第1節 質量保存の法則
この航空工学講座では時間で変化しない流れ(定常流れ)を考えます。航空機は加速したり旋回したりするので、そんな仮定は不十分だと思うかもしれませんが、流れの速さに対して、航空機の周りの流れの変化はゆっくりとなるため、時間で変化しないという仮定が十分に成り立ちます。もちろんこの仮定が成り立たない現象もありますが、今回の講座では扱っていません。
流れとは空間上の各点で流れの速度とその向きが決まる状態を指します。数学的には速度のベクトル場となります。また、流れの中に置いた仮想の点がたどる線のことを、流線と呼びます。
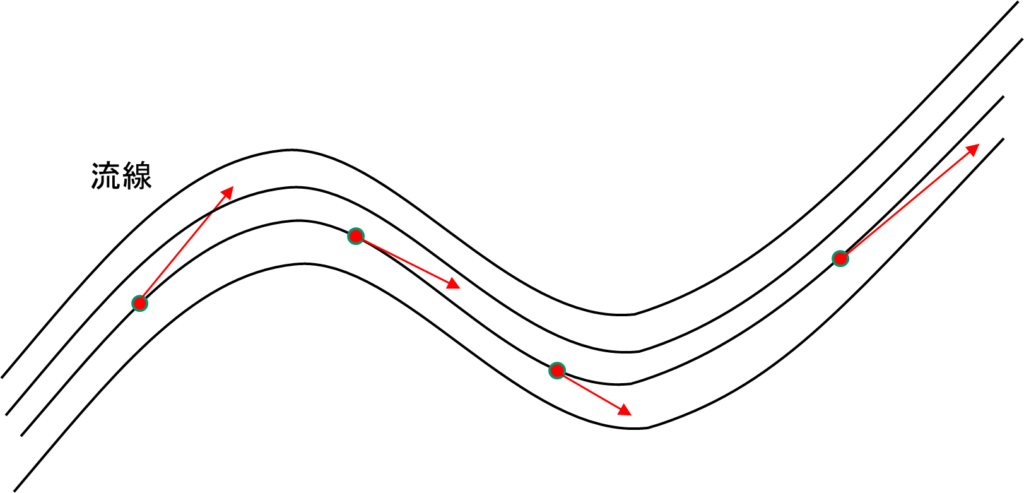
下図のような流れにおいて、時間\(\Delta t\)内に断面1と断面2を通過する質量は同じになります。なぜなら、断面1を通る質量の方が、断面Ⅱを通る質量よりも大きい場合は、間に挟まれた部分の質量がどんどん大きくなり、反対の場合はどんどん小さくなります。流れの状態は変わらないので、断面Ⅰと断面Ⅱを\(\Delta t\)時間で通過する質量は同じでなければなりません。
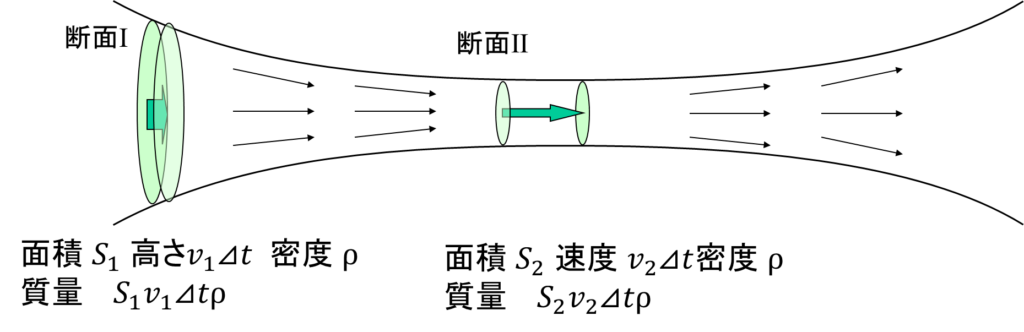
断面を通過する質量を計算してみましょう。この場合の体積は、\(\Delta t\)が小さいと仮定すれば、断面Ⅰと断面Ⅱを底面とする円柱とみなすことができるので、それぞれ面積を\(S_{1}\)、\(S_{2}\)、通過する高さは\(v_{1}\Delta t\)、\(v_{2}\Delta t\)、密度は同じで\(\rho\)とすると、次の式が成り立ちます。
$$S_{1} v_{1} \Delta t \rho=S_{2} v_{2} \Delta t \rho$$
つまり
$$S_{1} v_{1}=S_{2} v_{2} $$
このことは、流れの中で断面積\(S\)と速度\(v\)の積\(Sv\)が常に等しいことを指します。言い替えると広い部分を流れる流れはゆっくりと流れ、狭い部分を流れる流れは速く流れることを指します。川の流れを考えると、細くなっている部分は速く流れ、広くなっている部分はゆっくり流れるので当然の結果のようにも思えます。しかし、この性質は密度\(\rho\)が変化しないことを仮定した亜音速の流れで成立する話であり、密度が変化する超音速の流れでは成立しなくなります。その話は第5章の超不思議な超音速流れで説明するので、頑張ってそこまで理解してください。
第2節 ベルヌーイの法則
いよいよ航空機が飛行する原理の中心となるベルヌーイの法則について導いていきたいと思います。ベルヌーイの法則とはエネルギーの保存則を言い替えたものになります。下の図のような流れを考えます。
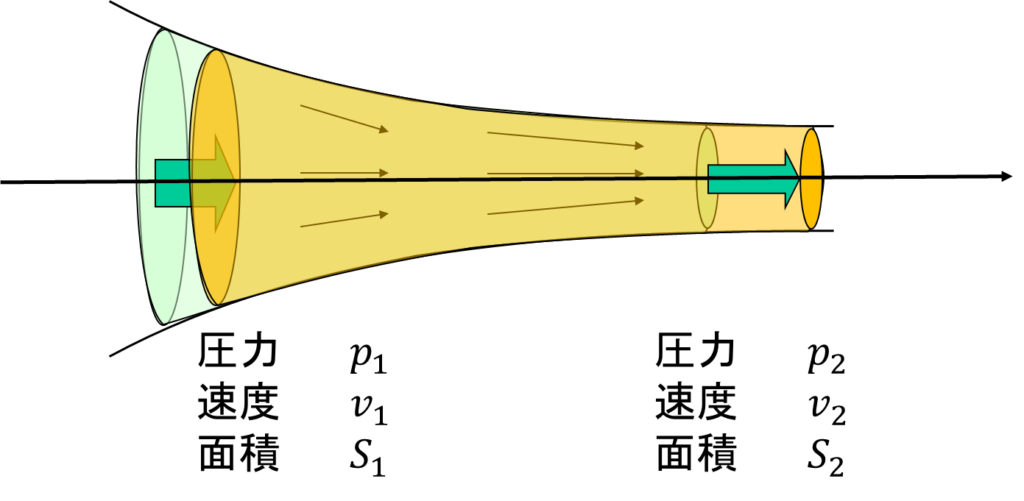
細くなっている管の中を左から右に流れていく流れのようにも見ることもできますが、ある流れの一部を考えていると思っても大丈夫です。大事なことは流れに沿った面から漏れ出さない、また中に入り込まない流れを考えているということです。
この流体に働く力として圧力だけを考えます。重力も考えるべきですが、一般的に空気のような密度が低い流れの場合は、重力の影響は無視できます。
この流れにおいて短い時間\(\Delta t\)秒の間に、緑色の流体がオレンジの流体まで移動したものとします。このとき
$$(流体がされた仕事)=(流体の力学的エネルギーの変化量)$$
が成り立ちます。
まずは右辺の力学的エネルギーの変化量から計算してみましょう。立体として重なっている部分の力学的エネルギーは同じになるので、引き算すれば消えることになります。そのため、次の図のように、力学的エネルギーの差は左右に重なっていない部分の力学的エネルギーの差になります。
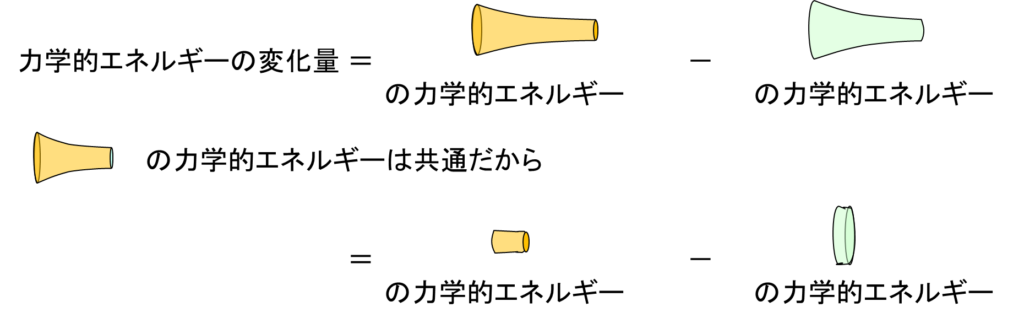
ここで質量保存の法則と同じように、それぞれ面積を\(S_{1}\)、\(S_{2}\)、通過する高さは\(v_{1}\Delta t\)、\(v_{2} \Delta t\)、密度は同じで\(\rho\)とすると、それぞれの力学的エネルギーを計算することができ、

$$(力学的エネルギーの変化量)=\frac{1}{2}\cdot S_{2}v_2\Delta t\rho\cdot v_{2}^{2}-\frac{1}{2}\cdot S_{1} v_{1}\Delta t\rho\cdot v_{1}^{2}$$
となります。
次に流体がされた仕事について考えてみます。流体がされた仕事は、下図のように考えられるため、
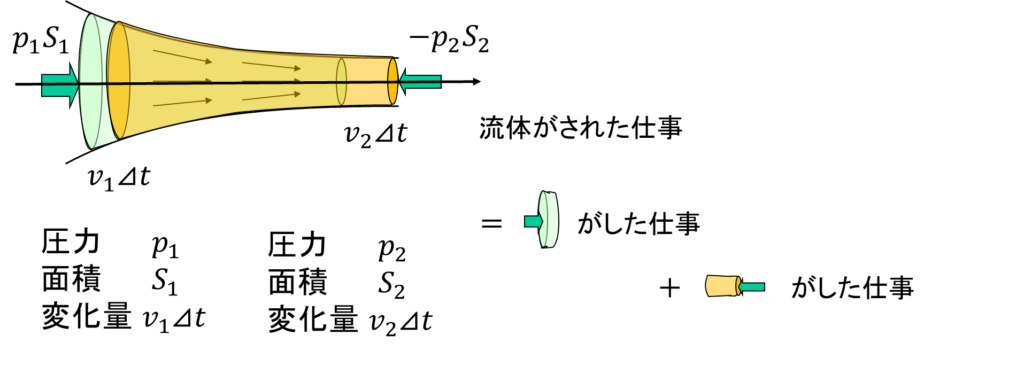
$$ \begin{align}(流体がされた仕事)& =p_{1} S_{1}\cdot v_2\Delta t+(-p_{2} S_{2})\cdot v_{2}\Delta t\\
&=p_{1} S_{1}\cdot v_2\Delta t-p_{2} S_{2}\cdot v_{2}\Delta t \end{align} $$
が得らます。
ここで(流体がされた仕事)=(流体の力学的エネルギーの変化量)が成り立っているので、
$$\begin{align} p_{1} S_{1}\cdot v_2\Delta t-p_{2} S_{2}\cdot v_{2}\Delta t &=\frac{1}{2}\cdot S_{2} v_2\Delta t\rho\cdot v_{2}^{2}-\frac{1}{2}\cdot S_{1}v_{1} \Delta t\rho\cdot v_{1}^{2}\\
p_{1} S_{1}\cdot v_{1}\Delta t+\frac{1}{2}\cdot S_{1}v_{1}\Delta t\rho\cdot v_{1}^{2}&=p_{2}\ S_{2}\cdot v_{2}\Delta t +\frac{1}{2}\cdot S_{2}v_2\Delta t\rho\cdot v_{2}^{2}\\
S_{1} v_{1} \Delta t\left(p_{1}+\frac{1}{2}\rho v_{1}^{2}\right)&= S_{2} v_{2} \Delta t\left(p_{2}+\frac{1}{2}\rho v_{2}^{2}\right)\end{align}$$
のように計算することができます。
また質量保存の法則\(S_{1}v_{1}=S_{2}v_{2}\)が成立しているため、結局、
$$ p_{1}+\frac{1}{2}\rho v_{1}^{2}=p_{1}+\frac{1}{2}\rho v_{1}^{2}$$
が成り立つことがわかります。
このことは下図のような流線上の各点で
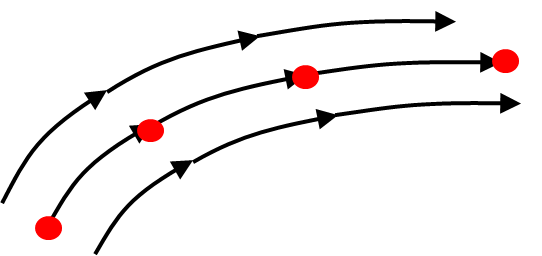
$$p+\frac{1}{2}\rho v^{2}=一定$$
が成立することを示しています。
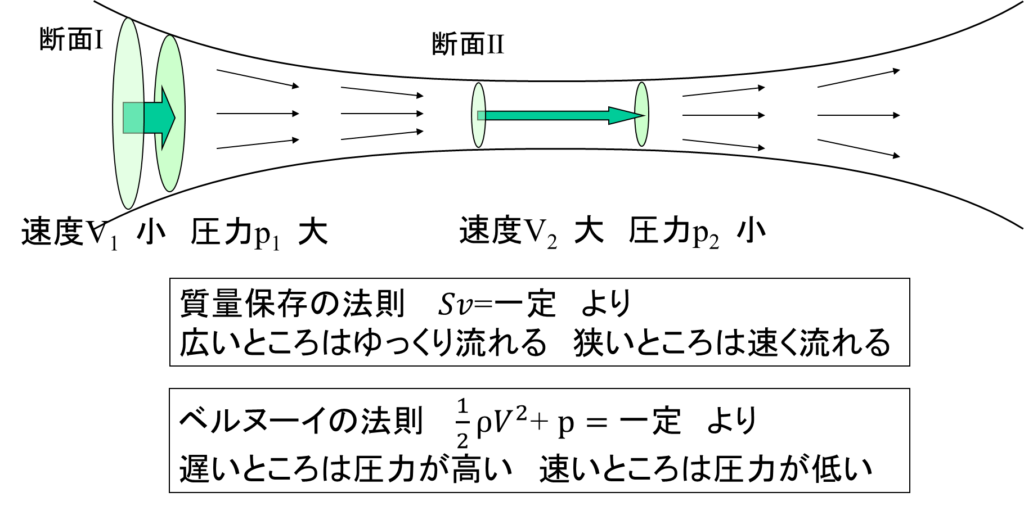
質量保存の法則とベルヌーイの定理をまとめると次のようになります。
第3節 揚力が働く仕組み
ベルヌーイの法則を導いたことで、揚力が働く仕組みについて説明する準備が整いました。下左図のような紙片を用意して、その上面に息を吹きかける簡単な実験をしてみてください。

実際に実験を行うと、紙片が浮き上がるのではないかと思います。この理由は、空気が摩擦力で引き揚げられたようにも感じますが、そうではありません。下図のように紙片の上部には空気が流れているため、ベルヌーイの法則により上面の圧力が大気圧より低下します。一方で、下側には流れがないため圧力は大気圧のままであり、結果として下側が大気圧で押すことになり、上側に持ち上がることが説明できます。
このことは次の図からわかると思います。

$$p_{1}+\frac{1}{2}\rho v^{2}=p_{2} より p_{2}-p_{1}=\frac{1}{2}\rho v^{2}≧0 $$
このことと同じ原理で航空機の翼は下側から押し上げられ、航空機を浮かせる力(揚力)が発生することになります。具体的に説明する前に、航空機の翼について、用語の説明をしておきます。ちなみに航空機の翼を「よく」と呼びます。
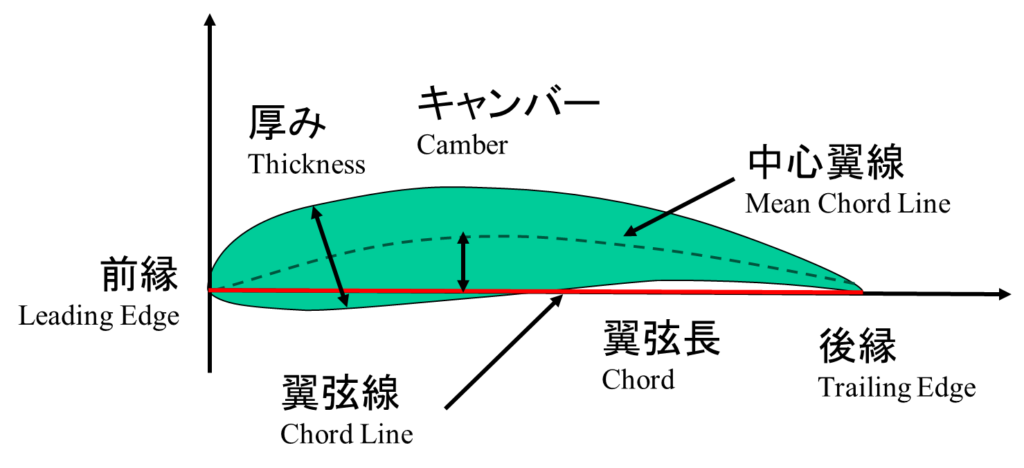
翼の名称
航空機の翼はいわゆる流線型と呼ばれる形をしています。この翼の中心を通る線を中心翼線といい、翼の一番先端部である前縁と一番後端部である後縁を結んだ線を翼弦線といいます。また翼弦線の長さを翼弦長といいます。よく見るとこの中心翼線は上側に反った形をしています。これは一般的な翼の特徴です。中心翼線が翼弦から一番離れた長さが翼の反り具合を表していますが、この値をキャンバーと呼びます。このキャンバーが翼に揚力を与える理由となっています。また、中心翼線から翼面までの距離が最も大きくなる大きさを厚みといいます。
揚力が発生する仕組み
翼の周りの流れについて考えてみましょう。翼の周りの流れは左下図のようになっていることが想像できます。左から来た流れは翼の上面と下面に分かれて流れ、また一緒になって右に流れていきます。ここで上側を流れる流れと下側を流れる流れを比べると、翼にキャンバーがあるため、上側を流れる流れの方が長い距離を流れていることになります。この流れは後縁で再び合流するため、上側を流れる流れの方が速い流れになっています。
ここでベルヌーイの法則の登場です。ベルヌーイの法則では、速い流れの方が圧力が小さくなることを示していました。つまり上面の圧力は下面の圧力よりも小さいことになります。実際には、場所によっても流れの速度は変わってくるため、圧力が変わってきます。その様子を示した図が右下図になります。圧力は面を垂直に押すため、このような図になります。

このように、上面を流れる流れの速度が、下面を流れる流れの速度より速くなることから、ベルヌーイの法則により下面の圧力が上面の圧力より大きくなり、翼を垂直に持ち上げる力が発生するのです。
このことはベルヌーイの法則が
$$ p_{1}+\frac{1}{2}\rho v_{1}^{2}=p_{2}+\frac{1}{2}\rho v_{2}^{2} $$
のようにあらわされることから、\(v_{1}>v_{2}\) ならば \(p_{1}<p_{2}\) であることを用いています。
マグナス効果
この原理を使うと野球やテニス、卓球等のスポーツにおいて、ボールが曲がる現象を説明することができます。
下図の左側のように、流れの中にある回転のないボールには、上下に同じ流れが生じます。一方で回転のある流れについては、下図の右側のように、回転により流れの回り込みが起きて、上下で非対称な流れになります。この図の場合は、ボールが時計回りに回転しているため、下側の流れが上側に回りこまされて、上面の方が流れる距離が長い、つまり速い流れになっています。

このため、上側の圧力が小さくなり、ボールは上側に持ち上がる軌道を描きます。実際には重力と相殺されるので、浮くというよりかは沈みにくい軌道(テニスでいえばスライス)になります。
このように移動しながら回転する物体に進行方向と垂直な向きに力が発生することを、マグナス効果と呼びます。
第4節 航空機に働く力
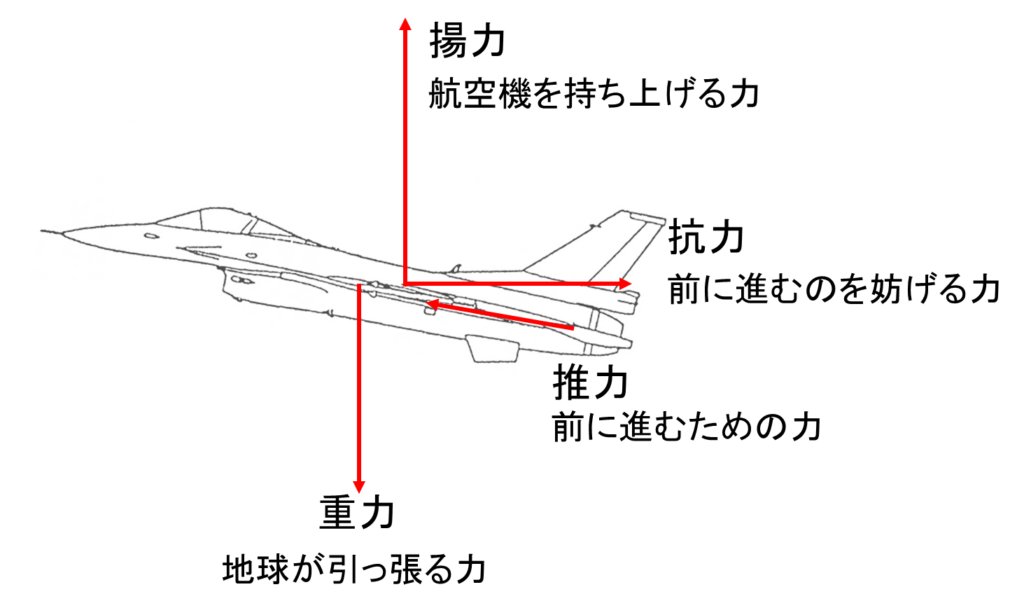
ベルヌーイの法則により、航空機には航空機を持ち上げる力「揚力」が発生することを説明しました。この力が重力とつり合い、航空機は遠くの目的地まで飛行できることになります。また、航空機には「抗力」と呼ばれる前に進むのを妨げる力も発生します。この力に打ち勝つために、エンジンが発生する前に進むための力「推力」が必要になります。それらをまとめたものが下図になります。
揚力や抗力の性質については、第4章で詳しく見ていくことします。
第5節 演習問題
練習問題1 現代の航空機でも速度を計測するために下図のピトー管を用いています。ピトー管の先端と両脇には孔が空き、先端で全圧(𝑃_𝑇)を、両脇で静圧(𝑃)をそれぞれ取得しています。両者は内部でつながりその部位の圧力の差を計測すれば、速度を求めることができます。(写真はSR-71のピトー管)

標準大気で高度0mを飛行したときに圧力の差が\(1500𝑁/𝑚^2\)となった場合、その時の飛行速度を求めなさい。ただし空気密度\(\rho\)は、\(\rho=1.225kg/m^3\)とします。
模範解答
ベルヌーイの法則から、
$$p+\frac{1}{2}\rho v^2=p_{T}$$
が成立するから、変形して、
$$\frac{1}{2}\rho v^2=p_{T}-p=1500$$
が成立する。
よって
$$v=\sqrt{\frac{1500\cdot 2}{1.225}}=49.5 m/sec$$
練習問題2 ピトー管が発明されるまでの1910年から1930年にかけては、飛行速度が低い航空機の速度計には以下に示すベンチュリー管が用いられていました。この装置は、管の内側の流れが機体の速度と同じになるような機体の場所を特定して、取り付けることが重要となります。
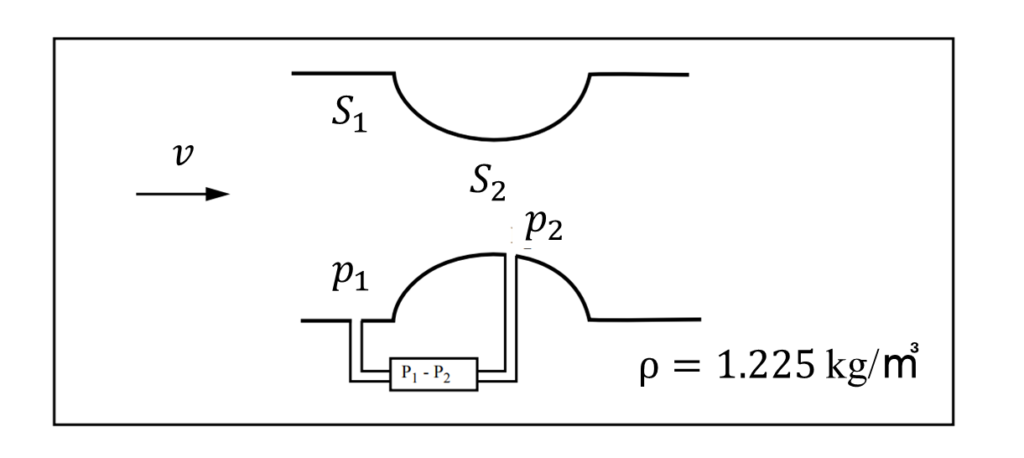
この図で\(S_{2}/S_{2}=4\)、 \(p_{1}-p_{2}=400 𝑁/𝑚^2\)となった場合の飛行速度を計算せよ。
模範解答
質量保存の法則から、
$$S_{1}v_{1}=S_{2}v_{2} より、\frac{v_{2}}{v_{1}}=\frac{S_{1}}{S_{2}}=4 つまり、v_{2}=4v_{1}$$
ベルヌーイの法則により、
$$p_{1}+\frac{1}{2}\rho v_{1}^{2}=p_{2}+\frac{1}{2}\rho v_{2}^{2} より p_{1}-p_{2}=\frac{1}{2}\rho v_{2}^2-\frac{1}{2}\rho v_{1}^2$$
\(p_{1}-p_{2}=400\)であることと、\(v_{2}=4v_{1}\)より、
$$800=15\rho v_{1}^{2}$$
\(\rho=1.225kg/m^{3}\)であるから、
$$v_{1}=43.5 よって v_{1}=6.6m/sec$$
