第1節 単位と次元
物理量の「単位」には、kg、m、sec等の「基本単位」や、その組み合わせによってできている「組み合わせ単位」があります。この基本単位の取り方はこの例以外にもg、cm、hrs等の別の単位を使うこともできます。
この基本単位の取り方によらずに、その単位の性質にだけ着目したものを次元といいます。例えばkg、g等の質量に関する次元はM(mass)で表し、m、cm等の長さに関する次元はL(length)で表し、秒、分、時等の時間に関する次元はT(time)で表します。また、組み合わせ単位の次元は、速度の場合\(LT^{-1}\)、密度の場合\(ML^{-3}\)のようになります。
以下に代表的な基本単位や組み合わせ単位と、次元の関係をまとておきます。
| 名称 | 単位 | 次元 | 名称 | 単位 | 次元 |
| 質量 | kg, g, lbs | M | 加速度 | m/sec2 | LT-2 |
| 長さ | m, cm, ft, NM | L | 密度 | kg/m3 | ML-3 |
| 時間 | sec | T | 力 | N(kg・m/sec2) | MLT-2 |
| 速度 | m/s, km/h, | LT-1 | 圧力 | Pa(kg/m・sec2) | ML-1T-2 |
第2節 空力係数
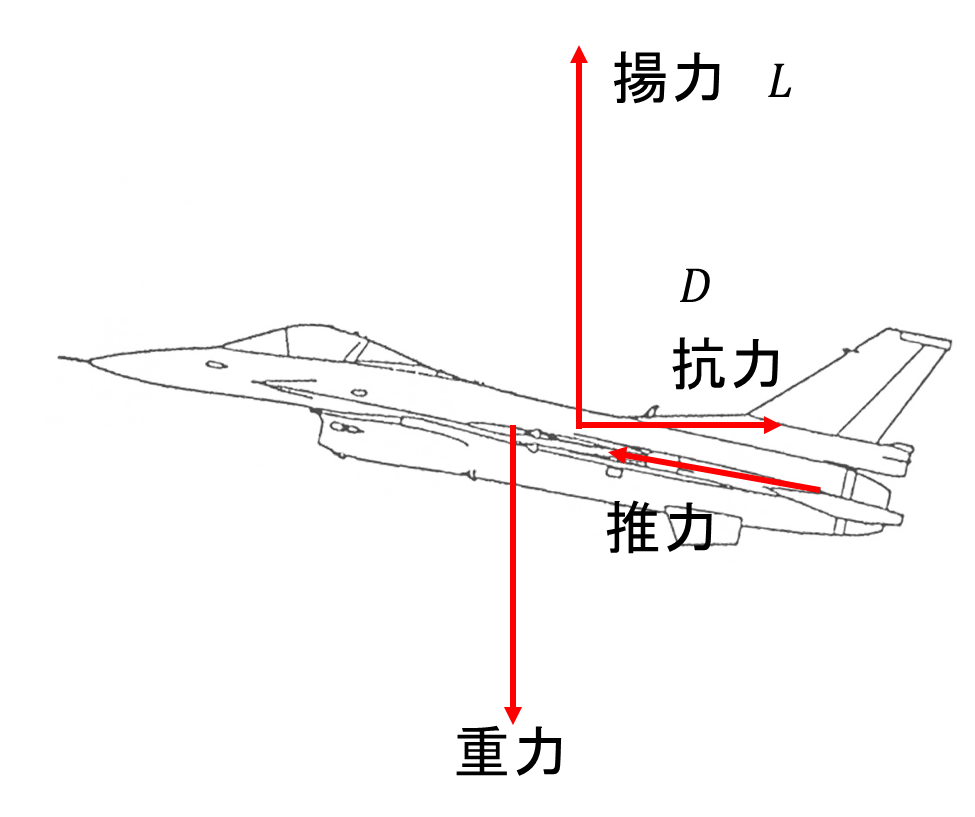
前回紹介した次の図において、揚力\(L\)と抗力\(D\)の空力係数\(C_{L}\)と\(C_{D}|)をそれぞれ次の式で定義します。
$$ C_{L}=\frac{L}{\frac{1}{2}\rho v^{2}\cdot S} 、C_{D}=\frac{D}{\frac{1}{2} \rho v^{2}\cdot S} $$
ここで\(S\)は翼面積になります。
第3節 相似則について
空力係数
一般的に航空機に働く力を求めるには、模型を使った風洞試験を行いデータを取得し、実際の機体に合わせた数値に変換していることは想像できると思います。では、具体的にどのような計算しているのでしょうか。

この計算のもとになる考え方が、相似則という考え方です。上の2つの写真は、同じ形状をした模型と実機の2つの機体が同じ飛行状態で飛んでいます。同じ飛行状態という説明は、少しあやふやですが、ここで詳しくは説明することはやめておきます。イメージしてほしいのは、流れに対して同じような角度で正対して飛行していることを指します。
このとき、模型と実機から計算された空力係数はある条件のもとで一致します。つまり、ある条件の下で、次が成立します。
$$C_{L_{m}}=C_{L_{r}} 、C_{D_{m}}=C_{D_{r}}$$
ここで、\(C_{L_{m}}、C_{D_{r}}\)は模型の空力係数、\(C_{D_{m}}、C_{D_{r}}\)は実機の空力係数を指します。
この関係を相似則と呼びます。それでは、相似則が成立する理由と、その「ある条件」について詳しく見ていきたいと思います。
相似則が成立する理由
一般に航空工学の世界に限らずに、工学の世界ではさまざまな相似則が成立する理由について、BuckinghamのΠ定理を用いて説明します。つまり、正しく理解するためにはΠ定理を理解する必要があります。しかし正確に理解するのは難しい定理です。ここでは、BuckinghamのΠ定理を表向き使わずに、相似則が成立する理由について考えていきたいと思います。
大きさは異なりますが、同じ形状と同じ飛行状態の2つの航空機に働く力を求める次のような式があると仮定します。
$$F=F(v, l, \cdots )$$
ここで、この関数は、風洞試験と実機に働く力を比較するために、速度\(v\)と大きさ\(l\)の関数であることを仮定しています。もちろんこのような関数を具体的に求めることは無理ですが、関数の性質を調べることは可能です。
まず、この関数は\(v\)と\(l\)の関数であることを仮定していますが、ほかにどのような変数を持つでしょうか?例えば、空気密度\(\rho\)の影響を受けそうなため、\(\rho\)を変数に持つと仮定できそうです。他にも圧力\(p\)や温度\(T\)も影響するように思います。しかし、圧力は求めたい力そのものであり、また圧力が変化することで空気密度\(\rho\)に影響を与えることから、この関数の変数としては除外しておきます。温度についても同様に考えて除外します。
このあたりの検討は、正解を知っているために正しい選択が簡単にできているわけですが、ゼロから議論をすると正しい答えを導くことは難しいと思います。この結果は、長い航空工学の歴史の中で取捨選択されたものだと考えて認めてください。
ほかに流れに影響を与える変数として、空気の粘度を表す粘性係数\(mu\)を追加しておきます。唐突ですが、空気の粘りっこさが航空機の周りの流れに影響を与えることは想像できると思います。以上から航空機に働く力\(F\)は
$$F=F(v, \rho, l , \mu )$$
と表されると仮定します。
本当は、さらに音が伝わる速さ\(a\)を含めて考えるのですが、今は遅い流れを考えているので、ここでは含めません。音速\(a\)まで含めた流れについては、第5章で考えるので楽しみにしていてください。
ここで今仮定した関数\(F(v, \rho, l , \mu )\)の性質を見ていきたいと思います。この関数はどんな式かは分かりませんが、\(v^{a} \rho^{b} l^{c}\mu^{d}\)という項の和であらわされていると考えます。この考え方をいきなり理解するのは難しいかもしれませんが、例えば三角関数や指数関数は、次のように展開できることは有名です。
$$\begin{align}\sin x&=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5+\cdots\\e^{x}&=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\cdots\end{align}$$
同じように考えれば、関数\(F(v, \rho, l , \mu )\)も\(v^{a} \rho^{b} l^{c}\mu^{d}\)という項の(無限の)和で表されると考えることができそうです。しかし、項\(v^{a} \rho^{b} l^{c}\mu^{d}\)の指数を自由に選ぶことはできません。なぜなら、次元をそろえる必要があるからです。
関数\(F(v, \rho, l , \mu )\)は力を表しているので、力の次元\(MLT^{-2}\)を持っています。つまり、この関数の項\(v^{a} \rho^{b} l^{c}\mu^{d}\)の次元が、力の次元\(MLT^{-2}\)になるように、指数\(a\)、\(b\)、\(c\)、\(d\)を選ばなければならないということです。それでは、このための条件を計算してみましょう。
まず、各変数の次元をまとめると次のようになります。
$$\begin{array}{|l|l|l|}
\hline
量&単位&次元\\
\hline
力:F&kg\cdot m/sec^{2}&M\cdot L\cdot T^{-2}\\
\hline
速度:v&m/sec&L\cdot T^{-1}\\
\hline
密度:\rho&kg/m^{3}&M\cdot L^{-3}\\
\hline
大きさ:l& m&L\\
\hline
粘性係数:\mu&kg/m\cdot sec&M\cdot L^{-1}\cdot T^{-1}\\
\hline
\end{array}$$
この表を用いて、項\(v^{a} \rho^{b} l^{c}\mu^{d}\)の次元を計算してみます。
$$\left[L\cdot T^{-1}\right]^{a} \left[M\cdot L^{-3}\right]^{b}\left[L\right]^{c}\left[M\cdot L^{-1}\cdot T^{-1}\right]^{d}=M^{b+d}\cdot L^{a-3b+c-d}\cdot T^{-a-d}$$
この次元が、\(MLT^{-2}\)に一致しないといけないので、
$$\left\{\begin{array}{rcc}
b+d&=&1\\
a-3b+c-d&=&1\\
-a-d&=&-2
\end{array}\right.$$
が成立しなければなりません。ここで\(d\)を固定して解くと、
$$\left\{\begin{array}{rcc}
a&=&-d+2\\
b&=&-d+1\\
c&=&-d+2
\end{array}\right.$$
が得られます。これを元の項に代入すると
$$v^{a} \rho^{b} l^{c}\mu^{d}=v^{-d+2} \rho^{-d+1} l^{-d+2}\mu^{d}=(v^2\rho l^2)\left(\frac{\mu}{\rho v l}\right)^d$$
となります。
つまり\(F(v, \rho, l , \mu )\)の各項は、\((v^2\rho l^2)\left(\frac{\mu}{\rho v l}\right)^d\)の項の和であらわされるので、次のような形になります。
$$F(v, \rho, l , \mu )=A_{0}(v^2\rho l^2)+A_{1}(v^2\rho l^2)\left(\frac{\mu}{\rho v l}\right)+A_{2}(v^2\rho l^2)\left(\frac{\mu}{\rho v l}\right)^2+\cdots$$
ここで右辺について\(v^2\rho l^2\)でくくると、
$$F(v, \rho, l , \mu )=(v^2\rho l^2)\left\{A_{0}+A_{1}\left(\frac{\mu}{\rho v l}\right)+A_{2}\left(\frac{\mu}{\rho v l}\right)^2+\cdots\right\}$$
となり、\(\left\{\cdot\right\}\)の中は\(\frac{\mu}{\rho v l}\)の関数になることから、
$$F(v, \rho, l , \mu )=(v^2\rho l^2)G\left(\frac{\mu}{\rho v l}\right)$$
のような形の関数でなければなりません。
さらに、\(\frac{1}{2}\rho v^2\)でまとめ、関数\(2G\)は、\(\frac{\mu}{\rho v l}\)の関数であることから、\(\frac{\rho v l}{\mu}\)の関数であるとも考えられるので、関数\(F\)は、
$$F(v, \rho, l , \mu )=\frac{1}{2}\rho v^2\cdot l^2\cdot G’\left(\frac{\rho v l}{\mu}\right)$$
のように表してもかまいません。
さらに\(l\)は航空機の大きさを表す変数したが、\(l^2\)は面積の次元を持ち航空機の大きさを表す変数になるので、\(l^2\)の代わりに改めて翼面積\(S\)を選べば、
$$F(v, \rho, l , \mu )=\frac{1}{2}\rho v^2\cdot S\cdot F\left(\frac{\rho v l}{\mu}\right)$$
と表されることが分かりました。※先に用いた関数\(G’\)も改めて、\(F\)と置きなおしています。
以上の議論から、形状や飛行状態が同じで、大きさが違う航空機に働く力は上記の形であらわされることが分かりました。このことは、形状や飛行状態が同じで大きさが違う航空機に対して発生する揚力や抗力から、以下の式で求めた空力係数がある条件の下で等しいことを指しています。
$$ C_{L}=\frac{L}{\frac{1}{2}\rho v^{2}\cdot S} 、C_{D}=\frac{D}{\frac{1}{2} \rho v^{2}\cdot S} $$
ここである条件というのは、2つの状況下での\(\frac{\rho v l}{\mu}\)が等しいことを指します。この値をレイノルズ数\(Re\)と呼びます。
$$Re=\frac{\rho v l}{\mu}$$
次の節ではレイノルズ数の性質について調べていきます。
第4節 レイノルズ数と境界層
風洞試験とレイノルズ数(その1)
先の節の計算から風洞試験の結果を用いて実際の航空機に働く力を求めるためには、空力係数を計算すればよいことが分かりました。ただしその場合の条件として、レイノルズ数を一致させる必要があることもわかりました。風洞試験と実機の飛行で、レイノルズ数を一致させるためには、どのようにすればよいか見ていきましょう。
まずレイノルズ数は次の形をしていました。
$$Re=\frac{\rho v l}{\mu}$$
つまり、模型のように、\(l\)が小さくなった場合、レイノルズ数を一致させる方法には、①\(v\)を大きくする、②密度\(\rho\)を大きくする、③粘性\(\mu\)を小さくする、の3つの方法があります。1つずつ見ていきましょう。
①\(v\)を大きくする
\(v\)を大きくすると空気が圧縮される影響が出てきます。空気の圧縮の影響は音として伝わるため、音速に近くなると大きな影響が現れます。この影響については、第5章で詳しくみていきますが、10分の1の模型を作ると、レイノルズ数を同じにするためには10倍の速度が必要となり、航空機の飛行速度を考えると容易に音速を突破してしまいます。このため、レイノルズ数を等しくする方法として(\v\)を大きくすることはあまり賢明な方法ではありません。
②密度\(\rho\)を大きくする
密度を大きくする方法は航空工学の発展期にはいろいろと研究されたようです。いかに示すゲッチンゲン風洞試験装置は、密度を高めた空気の流れを実現するために作られました。我が国においても、戦前の海軍で高圧風洞装置が作られて試験されたようです。
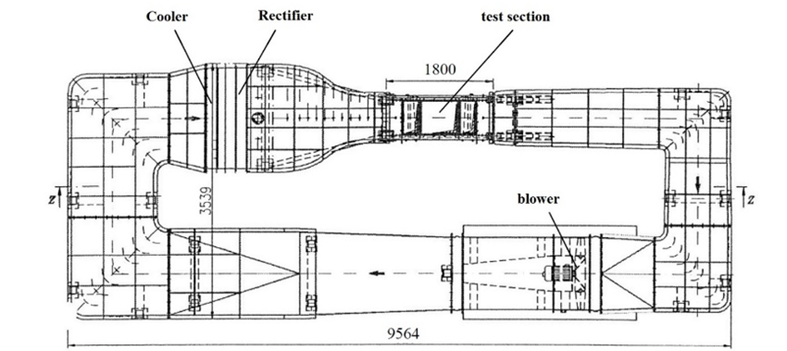
これらの風洞装置は密度を高めるために圧力を高めて試験を行うため、試験装置の実現が難しく、実現できてもさまざまな問題が発生したため、現在ではあまり使用されていません。
また同様の考え方で、液体を利用した試験も行われています。写真はNASAのWater Tunnelの写真です。
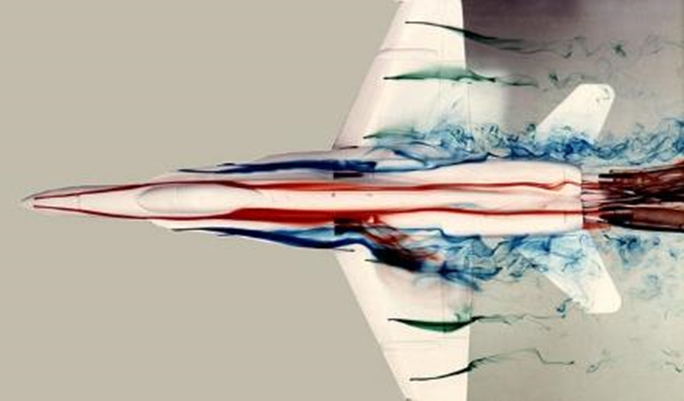
③\(\mu\)を大きくする
レイノルズ数を等しくするためには、模型に合わせて粘性係数を小さくすることでも実現可能ですが、粘性係数は温度の関数であり次の式で表されることが分かっています。サザーランドの式
$$\mu=\frac{1.4587\cdot T^{\frac{3}{2}}×10^{-6}}{T+110.4}$$
この式で粘性係数を10分の1にしようとすると極めて低温にしなくてはならないため、粘性係数を小さくすることでレイノルズ数をそろえることも妥当な方法とはなりません。
レイノルズ数と境界層
レイノルズ数の影響を調べるには、境界層について理解する必要があります。境界層とは物体付近に出来た流れの薄い層になります。平板の上を流れる流れは下図に示すように、最初は層流境界層を形成します。層流境界層はきれいな層を形成し、物体の表面に対して垂直方向には流れません。また、層流境界層は流れが進むにつれて徐々に厚くなっていきます。
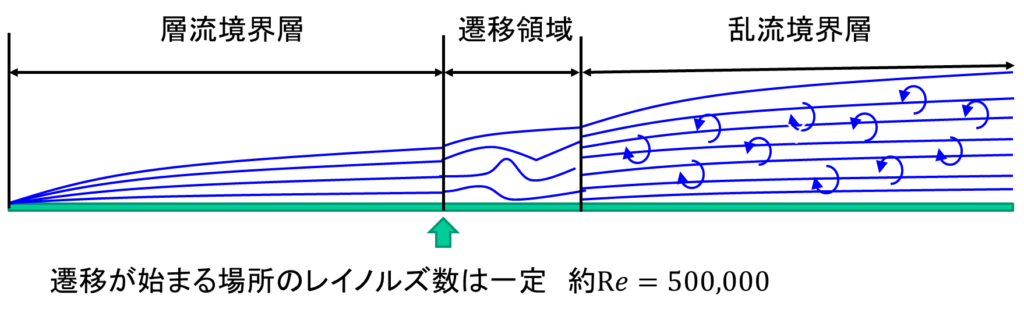
層流境界層はやがて、一時的な剥離を起こします。剥離とは物体表面に沿って流れなくなる状態を指します。この領域を遷移領域と呼びます。遷移領域を経た流れは物体の表面上を再び流れるようになります。この剥離を起こす場所は、流れの速度や密度、粘性係数により変化しますが、相似則を考えたらレイノルズ数が一定の場所で起きるはずです。実際にレイノルズ数で考えると、Re=500,000の時に遷移領域が始まることが知られています。
遷移領域を経て再び表面を流れるようになった流れは、今度は一定の流れではなく、時間で変化する流れとなり、また物体の表面に対して、垂直な方向にも流れるようになります。このような流れの層を乱流境界層と呼びます。
実際の翼面上の流れを可視化したものが次の写真になります。先に例を示した平板上の流れは、遷移領域で流れが一度剥離しますが、乱流境界層となって再び物体の表面を流れるようになりそのまま続きます。一方で、翼面上の流れは必ず最後に流れの剥離を伴います。この剥離が航空機の抗力の原因の1つとなります。流れの剥離に伴い増大する抗力を圧力抗力と呼びます。

もう一度、平板の上の流れを見てみましょう。今度は境界層の部分を拡大してみます。層流境界層と乱流境界層のそれぞれを拡大したときの境界層の速度分布は赤色の四角で拡大したようになります。ここで、乱流境界層の中の流れは時間で変化するため、時間平均をとったものになります。また平板の表面上の流れの速度はゼロになっていることにも注意が必要です。
2つの違いですが、層流境界層は境界層に垂直な方向に速度がゆっと変化しますが、乱流境界層は境界層の表面付近で急激に速度がゼロになります。この速度の変化が大きいほど表面摩擦力が大きくなるため抗力も大きくなります。つまり乱流境界層は、表面摩擦力による抗力を増大させることになります。
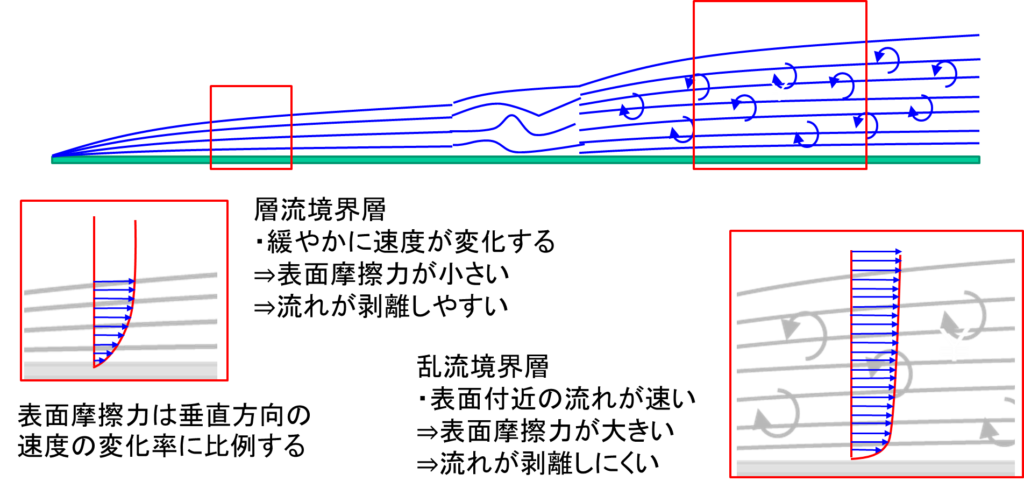
一方で、この変化が大きいことで表面付近まで速い流れとなり、流れが剥離しにくくなります。翼面上の流れでも見たように、流れは剥離する圧力抗力の原因となりますが、乱流境界層は剥離を抑えるため、剥離に起因する抗力の増大を抑えることにもなります。
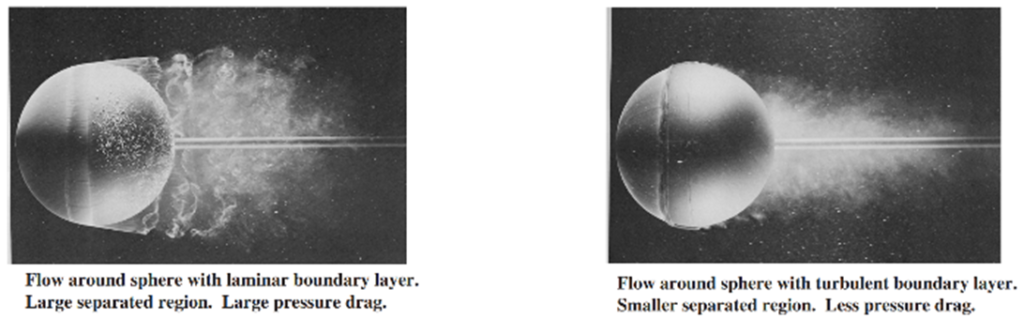
乱流境界層は剥離しにくいことを利用したものがゴルフボールにみられるディンプルというくぼみです。写真はwikipediaより

くぼみがないゴルフボールの流れは左下の図のように、急激なカーブで剥離してしまい圧力抗力を増大させています。一方で、乱流境界層により剥離しにくい流れは、右下の図のように境界層がボールの裏側まで回り込むことができ、圧力抗力の増大を抑えています。このため、ゴルフボールのくぼみがあることで圧力抗力の増大を抑え、ボールの飛距離を伸ばすことができるのです。(右下の図でディンプルは見られませんが、別の方法で乱流境界層を作っています。)
風洞試験とレイノルズ数(その2)
最後に、現在の風洞試験で高いレイノルズ数を実現するための工夫を紹介します。レイノルズ数の影響は、境界層に関する考察から分かる通り、流れの境界層やその遷移、そして剥離に関係してきます。またそれ以外には大きな影響を与えないこともわかっています。つまり、境界層や剥離を実機と同じように実現できれば、同じレイノルズ数で試験をすることと同じ効果が得られるのです。
そのための1つの方法として、左下の図のように風洞試験模型の先端にわずかな突起をつけることがあります。また場合によっては風洞試験模型の表面を荒くすることもあります。このような方法で人工的に層流境界層を乱流境界層に変異させて、高いレイノルズ数と同じ効果を実現します。これらの方法をラフネス法と呼びます。
また右下の図のように、風洞試験模型の前に格子をおいて風洞の中を流れる流れを乱しておく方法もあります。このような格子を乱流格子と呼びます。このような格子を用いることで、高いレイノルズ数で試験をする場合と同じ効果を得ることができます。
風洞試験ではこれらの方法を組み合わせて試験を行います。簡単に書いていますが、まこれらの貼り付け位置や突起の高さや表面の粗さ、格子の間隔などを適切な量に設定するには、非常に高い技術が必要となります。

第5節 演習問題
それでは実際に風洞試験データから、実機のデータに変換してみましょう。
演習問題1 風洞試験で測定したLとDのデータは以下のとおりであった。
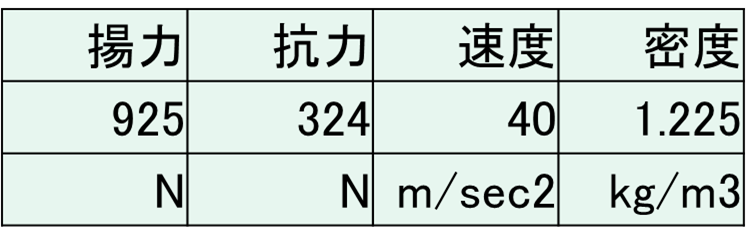
この時に、実機に働く揚力と抗力を求めよ。ただし、風洞試験模型の翼面積は\(0.56 m^2\)、実機の翼面積は\(22.44 m^2\)とし、実機の飛行条件は標準大気で高度\(3000m\)、飛行速度は\(100m/sec\)とする。

模範解答
まず空力係数を求めます。
$$\begin{eqnarray}
C_{L}&=&\frac{L}{\frac{1}{2}\rho v^2 S}=\frac{925}{0.5\cdot1.225\cdot40^2\cdot0.56}=1.69\\
C_{D}&=&\frac{D}{\frac{1}{2}\rho v^2 S}=\frac{324}{0.5\cdot1.225\cdot40^2\cdot0.56}=0.59
\end{eqnarray}$$
次に実機の揚力と抗力に変換します。
$$\begin{eqnarray}
L&=&\frac{1}{2}\rho v^2 S\cdot C_{L}=\frac{1}{2}\cdot 0.9095\cdot 100^2\cdot 22.66\cdot 1.69=174148\\
D&=&\frac{1}{2}\rho v^2 S\cdot C_{D}=\frac{1}{2}\cdot 0.9095\cdot 100^2\cdot 22.66\cdot 0.59=60797
\end{eqnarray}$$
以上の計算から17トン位の重量でも飛行することが分かります。ただし、6トン位の推力が必要になります。
風洞試験を行うためにもさまざまな風洞施設が用いられています。以下に示したのは、日本の代表的な風洞施設ですが、ほかにも様々な風洞施設が存在します。

