第1節 音とマッハ数と相似則
今までは空気は圧縮されないという前提でいろいろな現象をとらえてきました。しかし実際には空気は圧縮されます。特に高速で飛行する航空機の前縁部はピストンの先端のようになり、そこにある空気をどんどん圧縮していきます。圧縮された空気は音として周りに伝わっていきますが、速度が音に近づくと圧縮された空気は逃げることができずに、やがて衝撃波を発生させることになります。
こうなると今まで考えてきた空気力学は成り立たなくなります。また、空気は直感と異なるふるまいすらするようになります。ここでは不思議な超音速流れの性質について考えていきたいと思います。

マッハ数
航空機が静止状態であれば、音はすべての方向に同じ速さで伝わります。そのため音の波は左下の図のように同心円で広がっていきます。
次に航空機が移動状態であれば、音は移動した先の点を中心に広がるため、同心円とはなりません。下の真ん中の図のように、進行方向に圧縮された円を描きます。ただしこの場合は、航空機の移動速度が音の伝わる速度よりも遅い場合です。
最後に航空機が音が伝わる速度よりも速い速度で移動する場合を考えます。その場合は右下の図のように、音が広がるよりも先に航空機が移動してしまうため、移動した先の円は移動する前の円の外側に出来ることになります。またそれぞれの円の前面には水面を進む船のような波が発生しています。この波をマッハ波と呼びます。
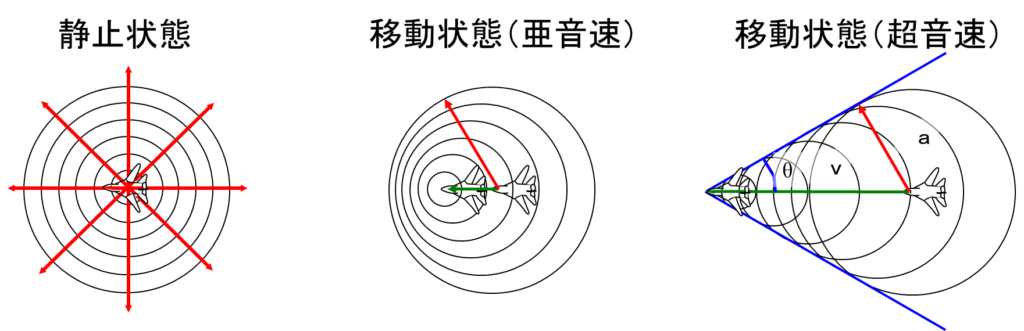
航空機が速度\(v\)で移動する場合、音の伝わる速さ(音速)を\(a\)とすると、
$$M=\frac{v}{a}$$
をマッハ数と呼びます。航空機が音よりも速く移動する場合、\(M>1\)となり、マッハ数は超音速での空気力学を考える際には非常に重要な変数となります。またマッハ波と航空機の進行方向のなす角\(\theta\)は、次のように計算することができます。
$$\sin\theta=\frac{a}{v}=\frac{1}{M}$$
なお、このマッハ波を衝撃波と説明する書物も多くありますが、マッハ波は最も弱い衝撃波であり、一般的な衝撃波とは異なることに注意が必要です。
音速を考慮した相似則
以上の検討から分かるとおり、圧力の変動が伝わる音速が流れの形状に大きな影響を与えます。つまり、第3章で考えた相似則について、音速\(a\)を加えた形で再検討する必要があるということです。そこで航空機に発生する力\(F\)が、
$$F=F(v, \rho, l , \mu, a )$$
と表されると仮定して、\(F\)がどのような形で表されるか再検討します。
第3章の検討と同じように考えると、この関数は、\(v^{a} \rho^{b} l^{c} \mu^{d} a^{e}\)という項の和であらわされなければなりません。しかしこの指数も自由に選べるわけではなく、それぞれの項の次元が力の次元\(MLT^{-2}\)と一致するように選ばなければなりません。
音速\(a\)を追加した、各変数の次元をまとめると次のようになります。
$$\begin{array}{|l|l|l|}
\hline
量&単位&次元\\
\hline
力:F&kg\cdot m/sec^{2}&M\cdot L\cdot T^{-2}\\
\hline
速度:v&m/sec&L\cdot T^{-1}\\
\hline
密度:\rho&kg/m^{3}&M\cdot L^{-3}\\
\hline
大きさ:l& m&L\\
\hline
粘性係数:\mu&kg/m\cdot sec&M\cdot L^{-1}\cdot T^{-1}\\
\hline
音速:a&m/sec&L\cdot \dot T^{-1}\\
\hline
\end{array}$$
この表を用いて、項\(v^{a} \rho^{b} l^{c}\mu^{d} a^{e}\)の次元を計算してみます。
$$\left[L\cdot T^{-1}\right]^{a} \left[M\cdot L^{-3}\right]^{b}\left[L\right]^{c}\left[M\cdot L^{-1}\cdot T^{-1}\right]^{d}\left[L\cdot T^{-1}\right]^{e}=M^{b+d}\cdot L^{a-3b+c-d+e}\cdot T^{-a-d-e}$$
この次元が、\(MLT^{-2}\)に一致しないといけないので、
$$
\left\{\begin{array}{rcc}
b+d&=&1\\
a-3b+c-d+e&=&1\\
-a-d-e&=&-2
\end{array}\right.$$
が成立することになります。ここで\(d\)と\(e\)を固定して解くと、
$$\left\{\begin{array}{rcc}
a&=&-d-e+2\\
b&=&-d+1\\
c&=&-d+2
\end{array}\right.$$
が得られます。これを元の項に代入すると
$$v^{a} \rho^{b} l^{c}\mu^{d}a^{e}=v^{-d+2} \rho^{-d-e+1} l^{-d+2}\mu^{d}a^{e}=(v^2\rho l^2)\left(\frac{\rho v l}{\mu}\right)^{-d}\left(\frac{v}{a}\right)^{-e}$$
となります。
つまり\(F(v, \rho, l , \mu, a )\)の各項は、\((v^2\rho l^2)\left(\frac{\rho v l}{\mu}\right)^{-d}\left(\frac{v}{a}\right)^{-e}\)の項の和であらわされることになります。
ここで第3章と同じように、\(l^2=S\)、\(\frac{\rho v l}{\mu}=Re\)、\(\frac{v}{a}=M\)と置いて整理すると、\(F(v, \rho, l , \mu, a )\)は次のような形でなければならないことが分かります。
$$F(v, \rho, l , \mu, a )=\frac{1}{2}\rho v^2\cdot S\cdot F\left(\frac{\rho v l}{\mu},M\right)$$
このことは、第3章での検討を踏まえると、空力係数はレイノルズ数の関数だけでなく、マッハ数の関数でもなけれななりません。つまり風洞試験の結果から、実機の空力係数を求めるためには、マッハ数も合わせて試験をしないといけないことを表しています。
実際に多くの風洞試験施設は、低音速風洞、遷音速風洞、超音速風洞と試験の目標とするマッハ数で分けて実施されます。
第2節 物理学の準備
圧縮性を考慮した空気力学を考えるためには、熱力学の知識等、より広範な物理学の知識が必要となります。この章で学ぶ内容については、基本的に高校生の知識で取り扱いが可能ですが、ここで証明するのは大変ですので、補講の章にまとめています。この節では事実として紹介のみ行います。細部は補講の章を確認してください。
| 気体の内部エネルギーの式 | \(U=nC_{v}T=\frac{pV}{\gamma-1}\) |
| 断熱変化の式 | \(p\rho^{-\gamma}=一定\) |
| 圧縮性ベルヌーイの法則 | \(\frac{\gamma}{\gamma-1}\frac{p}{\rho}+\frac{1}{2}v^2=一定\) |
| 音速の式 | \(a=\sqrt{\left(\frac{dp}{d\rho}\right)}\) |
断熱変化の式
左下のようなピストンを急に押すと右のように空気は圧縮され温度は上昇します。この変化の過程を断熱過程と呼び、圧縮性を考慮した空気力学では極めて大事な条件になります。
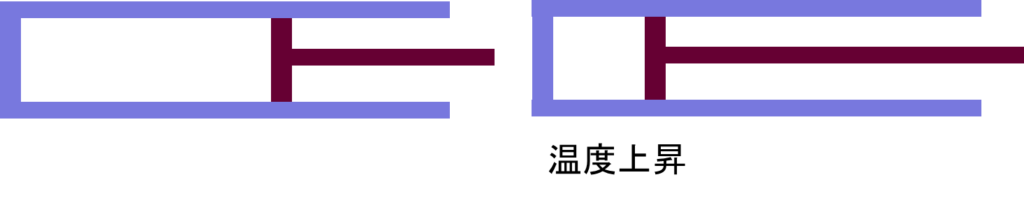
高校で習う物理学では熱力学の第1法則\(\Delta Q=\Delta U+\Delta W\)において断熱の仮定\(\Delta Q=0\)を使って式\(pV^{\gamma}=一定\)を導きます。
空気力学では、流れの中の体積を考えることは難しいため、次の流れの密度で表現した断熱変化の式を用います。
$$p\rho^{-\gamma}=一定$$
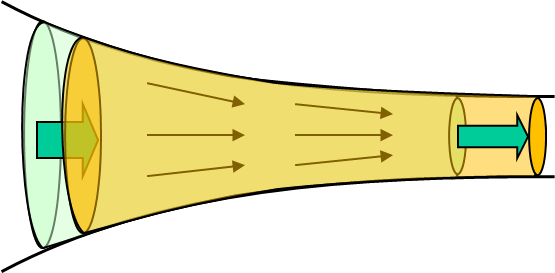
流れの中で以下のように粒子の塊が圧縮・膨張されながら流れていく様子をイメージするとよいと思います。

圧縮性ベルヌーイの法則
気体の圧縮性を考えない場合は
$$気体が受けた仕事=気体の力学的エネルギーの変化量$$
が成り立つことを利用して、ベルヌーイの法則\(p+\frac{1}{2}\rho v^{2}=一定\)を導きました。
圧縮性を考慮する場合は、気体の内部エネルギーも変化するため、
$$気体が受けた仕事=気体の力学的エネルギーの変化量+気体の内部エネルギーの変化量$$
と修正する必要があります。この関係式を使うと、圧縮性ベルヌーイの法則
$$\frac{\gamma}{\gamma-1}\frac{p}{\rho}+\frac{1}{2}v^2=一定$$
を導くことができます。
音速の式
音速は、圧力の変化が伝わる速度のことを指しています。この値は、空気の圧縮が無視できない速い流れ、特に超音速の流れでは、きわめて重要な値になります。
この値は、思考実験から
$$a=\sqrt{\frac{dp}{d\rho}}=\sqrt{\gamma RT}$$
のように求めることができます。
これらの式の導出については、補講「物理からの準備」を確認してください。
第3節 超不思議な超音速空気力学
準備
圧縮性を考慮しない流れでは、各断面の断面積を\(S_{1}, S_{2}, \cdots \)、速度を\(v_{1}, v_{2}, \cdots \)とすると、以下の質量保存の法則が成り立ちました。
$$S_{1}v_{1}=S_{2}v_{2}=S_{3}v_{3}=S_{4}v_{4}=S_{5}v_{5}$$
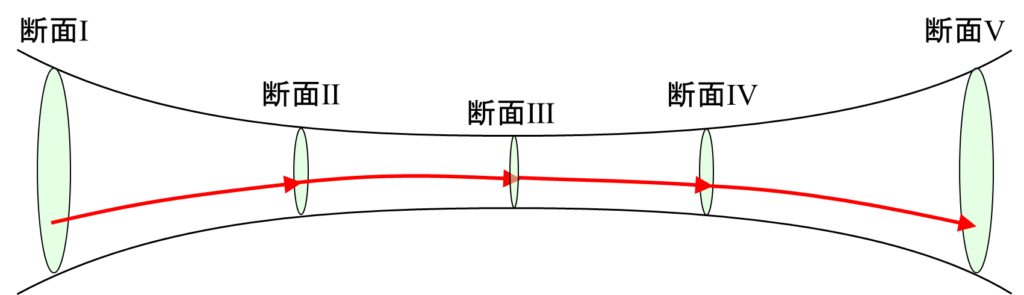
しかし、圧縮性の影響が出る超音速の流れでは成り立ちません。なぜなら空気が圧縮されることにより、密度が変化するためです。しかし各断面での密度を\(\rho_{1}, \rho_{2}, \cdots \)とすると、密度まで考慮した質量保存の法則
$$\rho_{1}S_{1}v_{1}=\rho_{2}S_{2}v_{2}=\rho_{3}S_{3}v_{3}=\rho_{4}S_{4}v_{4}=\rho_{5}S_{5}v_{5}$$
が成り立ちます。本来はこの式が質量保存の法則です。
それでは物理の準備や質量保存則を使って不思議な超音速流れの世界を見ていきます。以下のような流れの断面Ⅰと断面Ⅱにおける2つの断面での圧力、密度、断面積、速度をそれぞれ、\(p\)、\(\rho\)、\(S\)、\(v\)と、\(p+\Delta p\)、\(\rho+\Delta\rho\)、\(S+\Delta S\)、\(v+\Delta v\)とします。ここで\(\Delta\)と表しているのは、断面Ⅰと断面Ⅱの距離が小さく、変化量も小さくなっていることを仮定しています。

まず、ここで質量保存の法則が成り立つで、以下の式が成立します。
$$\rho S v=(\rho+\Delta\rho)(S+\Delta S)(v+\Delta v)$$
この式を展開して成立すると、
$$\rho S \Delta v+\rho\Delta S v+\rho \Delta S \Delta v+\Delta \rho S v+\Delta \rho S \Delta v+\Delta \rho \Delta S v+\Delta \rho \Delta S \Delta v=0$$
となります。今後よく使う計算方法ですが、\(\Delta\rho\)、\(\Delta S\)、\(\Delta v\)は小さいことを仮定しているので、それらの積はさらに小さくなり無視します。つまり、\(\Delta\rho\Delta S=\Delta\rho\Delta v=\Delta S\Delta v=\Delta S\Delta v=0\)とみなして、次のように変形します。
$$\rho S \Delta v+\rho\Delta S v+\Delta \rho S v=0$$
この式の両辺を\(\rho S v\)で割ると、次の式が得られます。
$$\frac{\Delta\rho}{\rho}+\frac{\Delta S}{S}+\frac{\Delta v}{v}=0$$
この式は後ほど使いますが、その前に同様な計算を圧縮性ベルヌーイの法則で行います。

先ほどと同様にこの断面で圧縮性ベルヌーイの法則を計算してみます。
$$\frac{\gamma}{\gamma-1}\frac{p}{\rho}+\frac{1}{2}v^2=\frac{\gamma}{\gamma-1}\frac{p+\Delta p}{\rho+\Delta\rho}+\frac{1}{2}(v+\Delta v)^2$$
ここで近似式\(\frac{1}{1-x}=1+x\)を利用します。すると、
$$\frac{1}{\rho+\Delta\rho}=\frac{1}{\rho}\cdot\frac{1}{1+\frac{\Delta\rho}{\rho}}=\frac{1}{\rho}\left(1-\frac{\Delta\rho}{\rho}\right)$$
が得られます。ここで、\(\frac{\Delta\rho}{\rho}\)は十分小さいことを利用しています。この式を圧縮性ベルヌーイの式に代入すると次の式が得られます。
$$\frac{\gamma}{\gamma-1}\frac{p}{\rho}+\frac{1}{2}v^2=\frac{\gamma}{\gamma-1}\frac{p+\Delta p}{\rho}\left(1-\frac{\Delta\rho}{\rho}\right)+\frac{1}{2}(v+\Delta v)^2$$
さらに展開して、2次の項を省略すると次の式が得られます。
$$\frac{\gamma}{\gamma-1}\left(\frac{\Delta p}{\rho}-\frac{p\Delta\rho}{\rho^2}\right)+v\Delta v=0$$
ここで、\(a=\sqrt{\frac{dp}{d\rho}}\)より、\(\Delta p=a^{2}\Delta\rho\)とし、さらに、\(a^{2}=\gamma RT\)と、\(p=\rho RT\)に注意して変形すると、
$$\frac{\Delta \rho}{\rho}=-\frac{v^2}{a^2}\cdot\frac{\Delta v}{v}=-M^2\frac{\Delta v}{v}$$
が得られます。この式に先の質量保存の法則から求めた式\(\frac{\Delta\rho}{\rho}+\frac{\Delta S}{S}+\frac{\Delta v}{v}=0\)を使って変形すると、次の式が得られます。
$$\frac{\Delta S}{S}=(M^2-1)\frac{\Delta v}{v}$$
この式が超音速での不思議な流れを理解するうえで非常に重要な式になります。この式の意味することについて考えていきます。
\(\frac{\Delta S}{S}=(M^2-1)\frac{\Delta v}{v}\)の解釈
先に出てきた図において右向きに進む流れを考えると、\(\Delta S\)の符号は次のように解釈することができます。
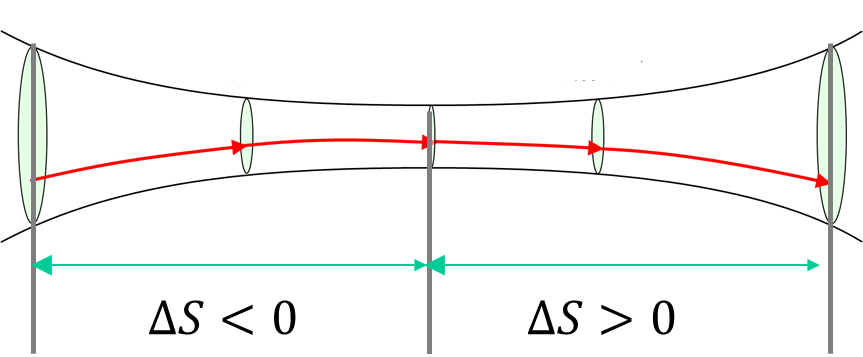
つまり、\(\Delta S<0\)は管の面積が小さくなる場合、つまり管が徐々に細くなる部分を指します。また反対に\(\Delta S>0\)となるのは、管が徐々に太くなる部分を指します。
ここで式\(\frac{\Delta S}{S}=(M^2-1)\frac{\Delta v}{v}\)について調べていきます。\(M<1\)の場合は、\(M^2-1<0\)となります。と言うことは、
\(\Delta S<0\)であれば、\(\Delta v >0\) ⇒ 細くなる部分で、流れは加速する。
\(\Delta S>0\)であれば、\(\Delta v <0\) ⇒ 太くなる部分で、流れは減速する。
という、当たり前な結論が得られます。しかし、この話は亜音速の場合です、次に超音速の場合を考えます。
超音速の場合は、\(M^2-1>0\)となるので、次のような結果が得られます。
\(\Delta S<0\)であれば、\(\Delta v <0\) ⇒ 細くなる部分で、流れは減速する。
\(\Delta S>0\)であれば、\(\Delta v >0\) ⇒ 太くなる部分で、流れは加速する。
という、直感とは異なる性質が得られます。またこれだけでなく、\(M=1\)を代入すると、\(\Delta S=0\)が得られます。
このことは何を意味しているかというと、管が一番細くなっている部分(くびれ部)でマッハ1になるということです。うそのような不思議な特徴ではないでしょうか。このよう性質は、実際に超音速流れで観測され、さまざまな面で活用されています。
CD管を利用した流れ
先ほどから考えている中央が細くなっている管のことをCD管と呼びます。細くなっている部分をConvergent管、広くなっている部分をDivergent管といい、結合したものをCD管と呼びます。この管は超音速の流れを作る際に非常に重要なものになります。

この管の左側の開口部の圧力を徐々に高めたときに、管の左から右に流れていく流れがどのように変化するかを考えていきます。
①亜音速の流れ
徐々に圧力を高くしていくと、くびれ部で速度が最大になり、また減速していきます。
②マッハ1の流れ
さらに圧力を高めていくと、Throat部でマッハ1に達します。D管では亜音速に戻ります。
③マッハ1を超えた流れ(その1)
くびれ部でマッハ1を達成した後、さらに圧力を高めていくと、流れはD管でも加速していきます。しかし、この加速はいつまでも続くとは限りません。ある場所で垂直衝撃波を発生させて、亜音速の流れに急激に減速します。このことをチョークと呼びます。またマッハ1が達成された以降は、C管の速度分布は断面積だけで決まりるため、圧力を上げても変わらなくなります。
④マッハ1を超えた流れ(その2)
さらに圧力を高めていくと垂直衝撃波が発生する位置が後退し、最後に反対側の開口部に到達します。この状態では、D管のすべての場所で超音速流れが達成されます。この場合も、C管と同様、D管の速度分布は断面積だけで決まります。
このような性質を利用したものに超音速風洞施設の吹き出し口があります。圧力を高めるだけでは、超音速の流れは達成できいないので、Throat部を設けてマッハ1を達成して、さらにマッハ数が高い流れを作りだしています。
くびれ部が分かる超音速風洞の図を探しています
ロケットエンジンのノズル形状
また、ロケットエンジンのノズルの形状もこの管の性質を利用しています。ロケットエンジンが高い推力を発生させるためには、できるだけ高い速度で燃焼ガスを噴射する必要があります。そのためにCD管を使って加速させています。
左下の写真はサターンロケットのエンジンノズル部になります。多くのロケットの燃料は液体水素と液体酸素になりますが、その燃焼ガスをこの細いノズルを通して短い時間で噴射して加速させていることになります。考えただけで、いかにロケットエンジンを作ることが難しい技術かが分かると思います。

なおCD管内部の速度は、チョークしない限り以下の式から断面積だけで決まります。
$$\frac{A}{A^{*}}=\frac{1}{M}\left[\left(\frac{2}{\gamma+1}\right)\left(1+\frac{\gamma-1}{2}M^2\right)\right]^{\frac{\gamma+1}{2(\gamma-1)}}$$
機会があればこの式の導出方法も紹介したいと思います。
第4節 衝撃波
以下のような写真(wikipediaより)が、音速を突破した瞬間や衝撃波が発生している等と紹介されていることがありますが、この写真から分かることについて説明したいと思います。

いろいろな記事で、先にも述べたマッハ波のことが衝撃波として紹介されています。マッハ波も衝撃波の1つですが、もっとも弱い衝撃波のことを指し、本当の衝撃波とは少し異なります。
本当の衝撃波は、垂直衝撃波と斜め衝撃波の2つに分類されます。どちらも圧力や温度、密度、マッハ数が不連続に変化する面を指します。厚みは極めて薄く、この面を通過すると、マッハ数\(M\)や圧力\(p\)、温度\(T\)、密度\(\rho\)が不連続に変化します。
垂直衝撃波
以下に示した簡単な図が垂直衝撃波を表していますが、衝撃波の前後で次のように変化します。
※結果のみ示しますが、できるだけ早く導出方法も紹介したいと思います。

$$M_{2}^{2}=\frac{(\gamma-1)M_{1}^{2}+2}{2\gamma M_{1}^{2}-\gamma+1}$$
$$\frac{p_{2}}{p_{1}}=\frac{1-\gamma+2\gamma M_{1}^2}{\gamma+1}$$
$$\frac{\rho_{2}}{\rho_{1}}=\frac{(\gamma+1)M_{1}^{2}}{2+(\gamma-1)M_{1}^{2}}$$
$$\frac{T_{2}}{T_{1}}=\left[\frac{2\gamma}{\gamma+1}M_{1}^{2}-\frac{\gamma-1}{\gamma+1}\right]\left[\frac{\gamma-1}{\gamma+1}+\frac{2}{(\gamma+1)M_{1}^{2}}\right]$$
ここで大事なことは、前後で次の関係があることです。
$$M_{1}>1>M_{2}、p_{1}<p_{2}$$
$$\rho_{1}<\rho_{2}、T_{1}<T_{2}$$
つまり、流れは超音速から亜音速に急激に減速されます、この減速に伴い、圧力や密度、温度も急激に上昇します。
斜め衝撃波
同様に斜め衝撃波とは、次のように流れが折れ曲がる場所に発生する衝撃波になります。

斜め衝撃波では、衝撃波に対して垂直な向きの流れで考えた場合、垂直衝撃波と考えられることから、垂直衝撃波の式を成分で考えた場合に、
$$M_{1}\longrightarrow M_{1}\sin\theta、M_{2}\longrightarrow M_{2}\sin(\theta-\delta)$$
で置き換えて、次の関係が成立することが分かります。
$$M_{2}^{2}\sin^{2}(\theta-\delta)=\frac{(\gamma -1)M_{1}^{2}\sin\theta^{2}+2}{2\gamma M_{1}^{2}\sin^{2}\theta^{2}-\gamma+1}$$
$$\frac{p_{2}}{p_{1}}=\frac{1-\gamma+2\gamma M_{1}^{2}\sin^{2}\theta}{\gamma+1}$$
$$\frac{\rho_{2}}{\rho_{1}}=\frac{(\gamma+1)M_{1}^{2}\sin^{2}\theta}{2+(\gamma-1)M_{1}^{2}\sin^{2}\theta}$$
$$\frac{T_{2}}{T_{1}}=\left[\frac{2\gamma}{\gamma+1}M_{1}^{2}\sin^{2}\theta-\frac{\gamma-1}{\gamma+1}\right]\left[\frac{\gamma-1}{\gamma+1}+\frac{2}{(\gamma+1)M_{1}^{2}\sin^{2}\theta}\right]$$
前後の関係は、同様に次のようになります。
$$M_{1}>M_{2}>1※、p_{1}<p_{2}$$
$$\rho_{1}<\rho_{2}、T_{1}<T_{2}$$
つまり、垂直衝撃波の場合と同じように、衝撃波により減速され、圧力や密度、温度が急激に上昇します。一方で、斜め衝撃波の場合は、ほとんどの場合、減速されても超音速を保ちます。※一部のケースで亜音速まで減速します。
また、\(\frac{p_{2}}{p_{1}}=1\)(\(\frac{\rho_{2}}{\rho_{1}}=1\)でもよい)とすると、\(\sin\theta =\frac{1}{M_{1}}\)が得られます。この角度はマッハ波の角度です。つまりマッハ波とは斜め衝撃波の中で、圧力が不連続に変化しない衝撃波となります。このことから、マッハ波は衝撃波として説明され間違いではないのですが、最も弱い斜め衝撃波と言われる理由になります。
以上の性質を踏まえて、航空機に発生する衝撃波について考えていきましょう。
次の写真は、NASAのホームページから取得した機体に発生した衝撃波を撮影した写真になります。一般に衝撃波は目に見えませんが、密度の変化を可視化することで、撮影したものになります。
機体の前方部には垂直衝撃波が発生し、外側に行くと斜め衝撃波になり、機体から離れた場所ではマッハ波となります。このマッハ波の角度からマッハ1.2くらいで飛行する航空機の写真であることが推測できます。音速を突破したといわれる航空機の写真とは、全く様子が異なるのではないかと思います。

もう少し翼面の流れについて詳しく見ていきたいと思います。
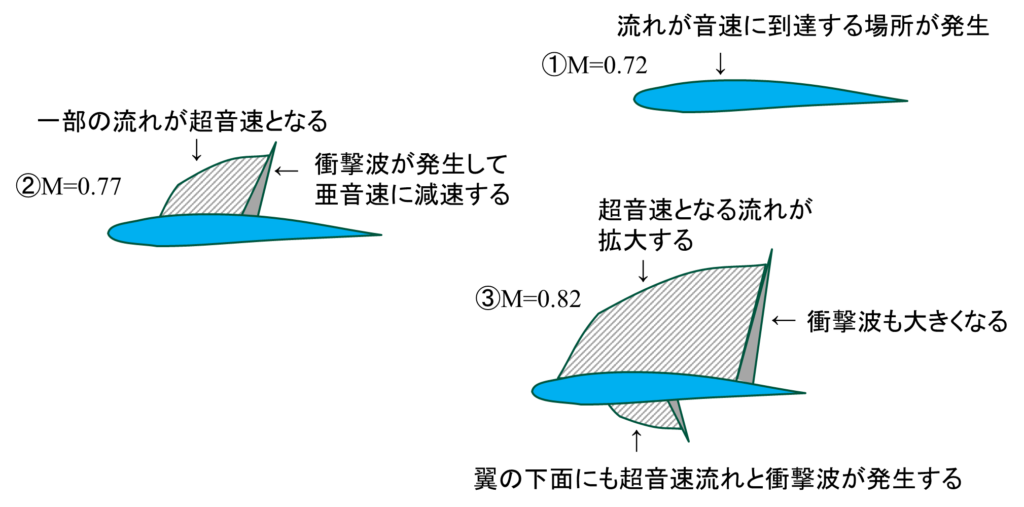
①M=0.72 機体の速度を徐々に上げていくと、翼面上のある点で音速が超える場所が現れてます。
②M=0.77 さらに機体の速度を上げると、翼面上に超音速で流れる領域が発生します。超音速に達した流れは翼の上面でさらに加速しますが、垂直衝撃波を発生させて亜音速まで減速します。
③M=0.82 機体の速度をさらに大きくすると、翼の下面にも超音速の流れが発生します。上面の流れと同様に加速されますが、最後は垂直衝撃波を発生させて亜音速まで減速します。
④M=0.95 マッハ数が0.95にまで達すると、翼面上のほとんどの領域で超音速の流れとなります。しかし機体の速度は亜音速のため、翼の後縁で垂直衝撃波を発生させ、亜音速に戻ります。
⑤M=1.05 機体の速度がマッハ1を超えるとほとんどの流れは超音速となります。しかし機体の前方部分には垂直衝撃波が発生するため、機体の前方部の一部には必ず亜音速の領域が発生します。この領域も翼面上で加速されて超音速流れに戻ります。
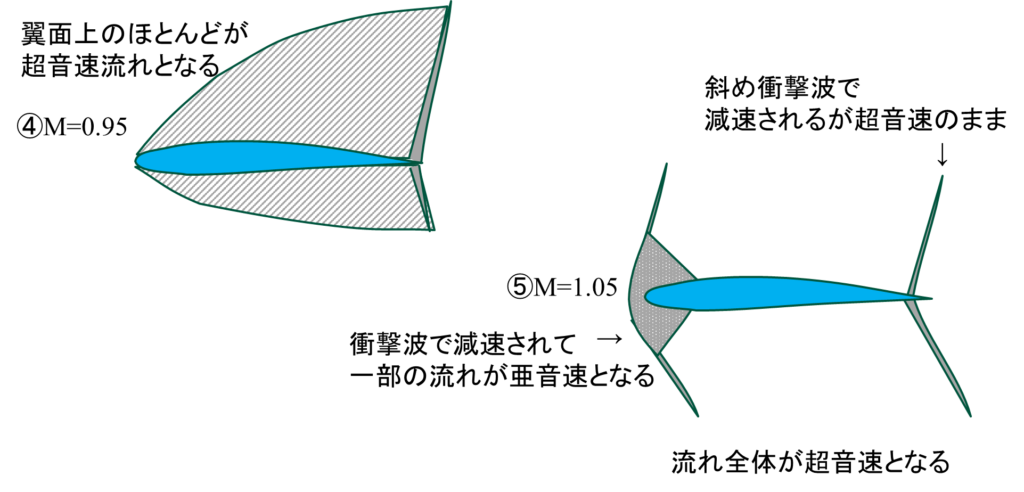
音速付近での流れの変化の様子は以上のように説明されます。
ここで最初に紹介した写真について考察していきたいと思います。ここで雲が発生している理由は、温度が下がり露点温度を下回ったためです。ではなぜ温度が下がったかと言うと、急激に流れが超音速まで加速されたことにより、気体が断熱膨張して圧力が低下し、温度も低下したためです。また反対に、雲の後ろ側では垂直衝撃波が発生して、一瞬で亜音速まで減速することで、気温がもとに戻ることから、雲は消失してしまっているのです。

翼面上の流れは音速を超えていると考えられますが、機体の速度としては音速を超えていません。とても印象的な写真ですが、音速を超えたとか言わないようにしましょう。
第5節 空力加熱
もう1つ超音速流れについて、誤解されやすいことについて説明します。以下は、某有名アニメ機動戦士ガンダム第5話「大気圏突入」の1シーンです。

ガンダムに限らず、宇宙から大気圏に入ってくる物体に発生する熱について、大気との摩擦と表現されることがよくありますがその表現は間違っています。正確には大気との摩擦ではなく、物体がピストンのように大気を押すのですが、速度が高すぎるために押された大気が逃げることができず、圧縮されて温度が上昇しているのです。この現象を空力加熱と呼びます。
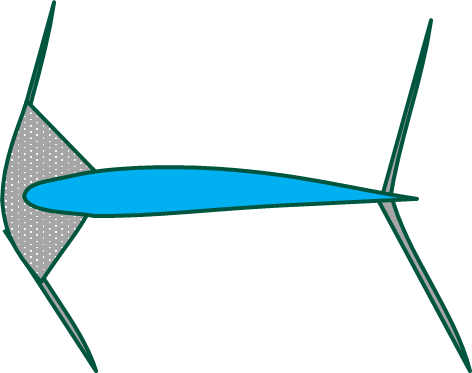
下の図のように、物体の前方では流れは速度ゼロまで減速されています。この点を淀み点と呼び、その温度を淀み点温度 \(T_{T}\) と呼びます。この淀み点温度について計算してみましょう。
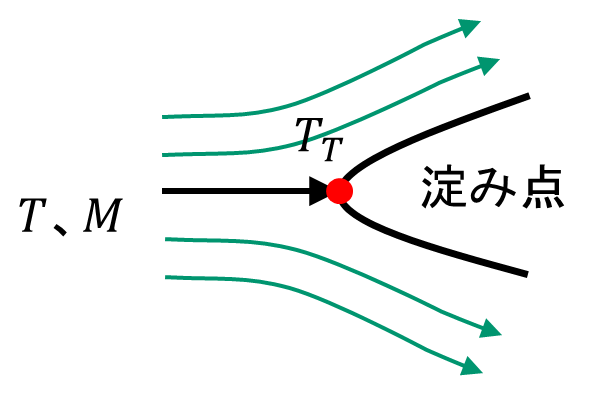
まずは圧縮性のベルヌーイの法則から、次の式が成立します。
$$\frac{\gamma}{\gamma-1}\frac{p_{1}}{\rho_{1}}+\frac{1}{2}v_{1}^2=\frac{\gamma}{\gamma-1}\frac{p_{T}}{\rho_{T}}$$
ここで、\(p=\rho RT\)、\(v=a\cdot M=\sqrt{\gamma RT}\cdot M\)であることから、
$$\frac{T_{T}}{T_{1}}=1+\frac{\gamma-1}{2}M^{2}$$
が得られます。
この式の値を実際に計算してみましょう。温度は成層圏を仮定して、\(T=-56.5(℃) = 216.65 (K)\)としておきます。すると、マッハ1では大した数字ではありませんが、X-15が飛行したマッハ5や、宇宙船が大気圏に突入する際の速度マッハ20では、以下のとおり、とんでもない温度になるのが分かります。
M=1.0 のとき \(T_{T}=1.2T=-13℃\)
M=5.0 のとき \(T_{T}=6.0T=1026℃\)
M=20 のとき \(T_{T}=81T=17276℃\)
この数字は、断熱圧縮という仮定の下で計算したため非常に高い温度を示していますが、実際には熱の移動や化学反応、熱の放射等の非常に複雑な現象を引き起こすため、これほど高い温度にはなりません。しかし、空力加熱による熱の上昇は、現在でも大きな技術的な課題となっています。
※超音速流れにおいては淀み点の前に垂直衝撃波が発生するため、正確な淀み点温度の計算のためには、垂直衝撃波による温度の変化を考慮する必要があります。
第6節 問題演習
作成中
