前回は芸能人格付けチェックで正解数が少ないことを知って、2枚買った宝くじが2枚とも当たるくらいの確率であることを確認してみました。もう少し深堀してみたいと思います。
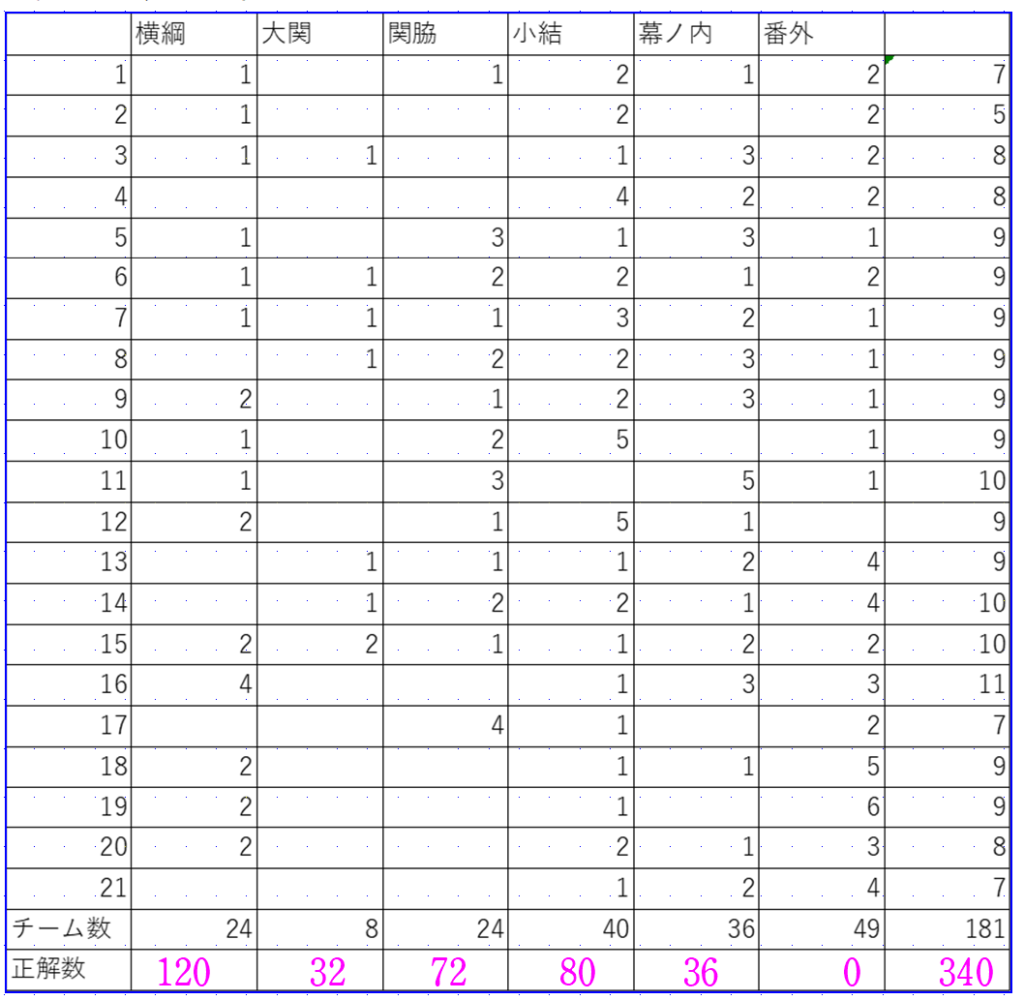
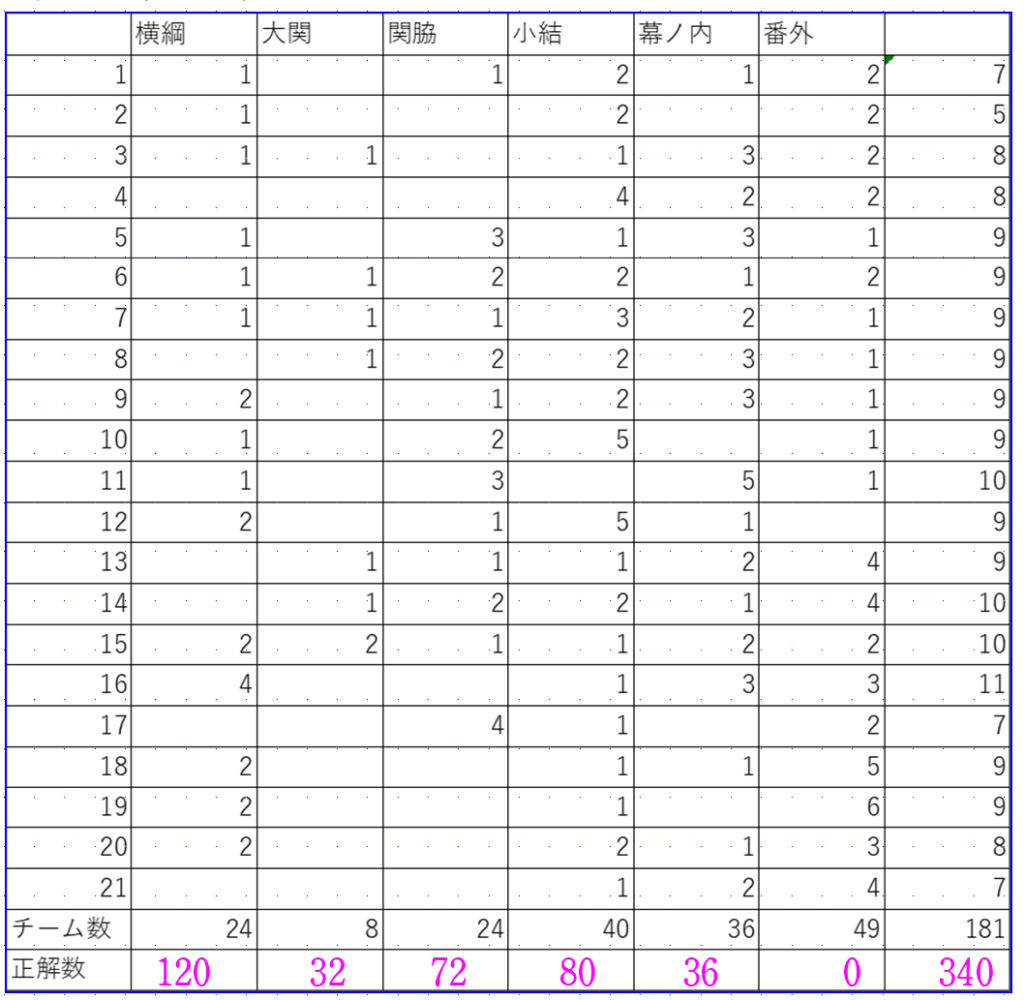
もう一度、この表を見てみます。すると、全問不正解で写す価値なし(番外)となったグループが49もあることが分かります。毎回5問に挑戦しているので、勘で答えても全問不正解になる確率は1/32になります。181チームが勘で挑戦したら、181×1/32=5.7から、全問不正解のグループ数はだいたい6グループになります。
そこで前回と同様に、次の問題を考えます。
181グループが2択の問題5問に勘で答えたとき、全問不正解のグループ数が49以上となる確率を求めよ。
勘で答えたときに全問不正解になる確率は、1/32であることから、全問不正解のチーム数が49以上になる確率は、次のように表すことができます。
$${}_{181}C_{49}\left(\frac{1}{32}\right)^{49}\left(\frac{31}{32}\right)^{132}+{}_{181}C_{50}\left(\frac{1}{32}\right)^{50}\left(\frac{31}{32}\right)^{131}+\cdots+\left(\frac{1}{32}\right)^{181}$$
になります。数列の\(\Sigma\)記号を使えば、次のように表現することができます。
$$\sum_{i=49}^{181}{}_{181}C_{i}\left(\frac{1}{32}\right)^{i}\left(\frac{31}{32}\right)^{181-i}$$
Wolfram Alphaに頼って計算すれば、だいたい\(1.56×10^{-31}\)という値になります。
sum(combination(181,i)*(1/32)^i*(31/32)^(181-i),(i,49,181)) – Wolfram|Alpha (wolframalpha.com)
その1で計算した確率\(3.60×10^{-14}\)の2乗よりもはるかに小さい値になっています。宝くじで考えると宝くじを4枚買ったときに4枚とも当たる確率よりも小さな値になります。またガンジス河にある砂粒の数が\(10^{20}\)個という推定(恒河沙という位は\(10^{52}\)を表し、ガンジス河のほとりの砂粒の数を意味しているといわれていますが、ちょっと盛りすぎです。)がありますが、その逆数よりもはるかに小さい値です。
つまりガンジス河(どうせなら地球上)に落とした砂粒1つを見つける確率よりもはるかに小さい確率ということになります。僕らは神仏でしか起こせないような奇跡を今目の前で目撃しているのです。浪漫がありますよね。さらにこの奇跡を伸ばしていってほしいと思います。
(その1)と(その2)を共通テスト風対話形式の授業教材にしたものが次のファイルです。