第1節 航空機発展の歴史
航空機発展の歴史は1903年にノースカロライナ州キティーホークでライト兄弟がライトフライヤー号で人類で初めて飛行したことに始まると考えがちですが、必ずしもそうではありません。実際にはライト兄弟の成功の12年前には、リリエンタールによる滑空飛行が成功し、それ以降、滑空飛行の研究は盛んにおこなわれ、その技術の蓄積の結果、ライト兄弟による動力飛行による初飛行につながっているのです。

また、それらの歴史は重航空機と呼ばれる空気より重い航空機の飛行に関する発展の歴史です。それ以前には空気よりも軽い軽航空機と呼ばれる気球の歴史もすでに始まっていました。1783年にはモンゴルフィエ兄弟によって熱気球を用いた初飛行に成功しています。またそれ以降、8000m以上の高度まで飛行した記録や事故によって亡くなった方の記録も残されています。
一般的に航空機の歴史は、ライト兄弟の成功から始まっていると考えられていて、その成功をきっかけとした爆発的な技術の進歩は目覚ましいものがありますが、その以前にも空を目指した人類の歴史があったことを知っておくことも大事なことではないかと思います。
一方で、ライト兄弟による人類初の動力飛行の成功後には、飛躍的な技術の進歩が見られます。特に第2次世界大戦直後から冷戦にかけては、技術が飛躍的に進歩し、当時建てられた記録がいまだに破られずに残っています。特に象徴的な出来事としては、1947年に達成されたチャック・イェーガーによる人類初の超音速飛行が挙げられると思います。当時は空気力学に対する知見も十分になく、超音速での飛行に関してはわからないことが多くありました。
そんな試行錯誤の時代には、誰も飛ばしたことがない航空機の特性は、実際に飛ばしてみるまで誰にもわかりませんでした。しかし、そんな航空機も誰かが最初に飛ばさないといけません。そのためのパイロットがテストパイロットと呼ばれる人々です。つまり航空機開発の歴史を作ったのは、テストパイロットであるといえるかもしれません。

チャック・イェーガーの超音速飛行の成功後は、飛躍的に速度記録や高度記録を伸ばしていきました。その象徴的な出来事は1963年にX-15というNASAの実験機で達成された高度107.8kmは、速度はマッハ6.7にまで達していて、速度記録はいまだに破られていません。
その後、航空機の発展の歴史は数字上は、大きな進歩はありませんが、2000年以降、民間航空機の分野で大きな発展がみられています。特にスペースシップワンが2004年に高度112kmを達成し、X-15による記録を破っています。一般的に、高度100km以上が宇宙とされていますが、今では民間人を対象とした宇宙飛行サービスが提供されています。
先に説明したチャック・イェーガーは日本ではあまり知られていませんが、アメリカでは英雄としてよく知られた歴史上の人物の一人です。平成3年には来日して岐阜基地を訪問し、当時防衛庁が開発したばかりのT-4中等練習機に搭乗しています。また休日には岐阜県根尾市大河原付近で釣りを楽しまれたとのことです。
残念ながらチャック・イェーガー氏は2020年にその生涯を閉じられますが、イェーガー氏の偉業を祈念して、根尾川で魚釣りをされた場所を見つけて同じ写真を再現しました。著作権上、元の写真は使えないので、ご容赦ください。それにしても、根尾市大河原はかなり山奥にあり、ここまで連れて行った岐阜基地のパイロットもすごいと思います。

以下、航空機の発展の歴史について速度記録や高度記録の点で簡単にまとめました。まさに今は宇宙開発も含めて、民間技術による発展の時代だと思います。

第2節 お空の話
航空工学について学ぶためには、空のことについて正確に知る必要があります。まず大事なことは、雨が降ったり、雷が鳴ったり雲が発生したりする大気現象はすべて対流圏という場所で起きているということです。対流圏は季節や緯度によって変化しますが、だいたい高度11kmまでです。それ以上の高さでは基本的に大気現象は発生せず、常に晴れた状態になっています。その場所を成層圏と呼びます。一般的に成層圏は高度50kmまでを指します。また対流圏と成層圏の間を対流圏界面と呼びます。旅客機が飛行する高度はこのあたりが多いと思います。
また高度が高くなるほど気圧が低くなり、酸素が薄くなります。酸素の濃度に変化はないため酸素が薄くなるという表現は正確ではありません。正確には酸素の分圧が低くなり、必要な量の酸素を体内に供給できなくなるといった方が正しい表現になります。旅客機の場合は航空機の中の圧力を高くして酸素分圧を高くしています。戦闘機でも同様にコックピットの中の圧力を高くしていますが十分ではなく、また圧力が下がる可能性もあるため普段から酸素マスクを着用し、濃度が高い酸素を供給して適切な酸素分圧を維持するようになっています。
さらに高度が高くなり高度20kmを超えると、水の沸点が低下して体温と同じ温度になります。この高度をアームストロングラインと呼びます。このため高い高度を飛行する場合は、さらに与圧服と呼ばれる宇宙服のような服を着て航空機に乗らなければなりません。
なお戦闘機に搭乗するためには、次の図の右上にある写真のような与圧室の中に入って減圧された状態を体験する航空生理訓練を受けなければなりません。訓練では実際に高高度まで減圧された状態を体験します。管理人が体験した訓練では、高高度と同じ気圧まで減圧した状態で酸素マスクを外し低酸素状態を体験しました。血中酸素濃度がみるみるうちに低下していき意識がなくなる寸前で、マスクを着用しました。

次に示したグラフが高度による気圧や空気密度、気温、音速の変化を表したグラフになります。今回の章の目標は、このグラフを描くことにあります。
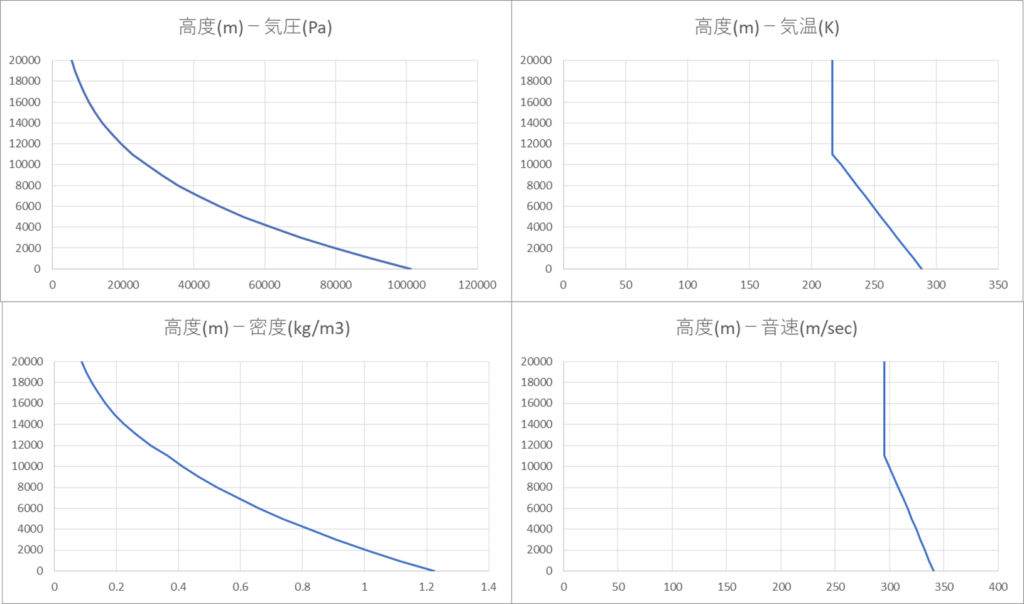
第3節 標準大気
標準大気の定義
航空機の性能を比較したり評価したりする際に、大気の定義がばらばらだと困ります。そのため国際民間航空機構(ICAO)が標準となる大気の性質を定めたものが、国際標準大気(ISA)になります。標準大気は次のように定義されます。
1 重力加速度は緯度、高度によらず一定
重力加速度 \(g=9.80665 m/sec^2\)
2 状態方程式 \(p=\rho 𝑅𝑇\) が成立
気体定数 \(𝑅=287.05287 J/kg\cdot K\)
3 対流圏の温度低減率は \(0.0065℃/m\)
成層圏の温度は一定
\(h≦11000m\) のとき \(T=288.15−0.0065h\)
\(11000≦h≦20000m\) のとき \(T=216.65\)(−56.5℃)
4 対流圏界面の高度11000m
5 海面上の標準状態は
圧力:101,325Pa 温度:288.15(K)(15℃)
※密度は、状態方程式より、1.225 kg/㎥と決まります。
状態方程式
一般に状態方程式は\(PV=nRT\)を用いますが、空気力学では\(p=\rho RT\)を用います。理由は体積という量を使わないからです。
この式を導くためには、分子量と質量の式\(w=nM\)を用いて、
$$PV=\frac{w}{M}RT$$
と変形します。ここで、\(\rho =\frac{w}{V}\)であり、改めて気体定数を\(\frac{R}{M}=R’\)とすると、
$$p=\rho R’T$$
が得られます。ここで航空機工学の世界では、圧力として大文字\(P\)ではなく、小文字\(p\)を用いることが多いので、小文字\(p\)を用いました。今後は、小文字\(p\)で統一します。
また空気の平均分子量は、次に示した空気の容積比の表から次のように求めることができます。
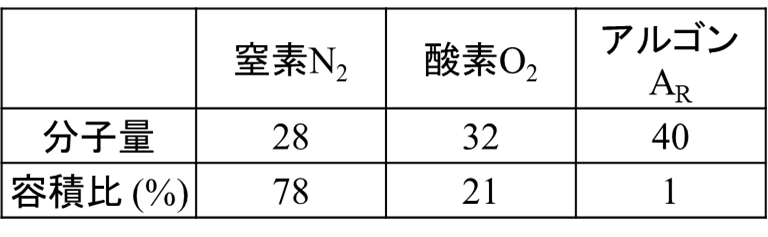
$$\frac{28×78+32×21+40×1}{100}=28.96$$
よって気体定数\(R’\)は
$$R’=\frac{R}{M}=\frac{8.31×10^3}{28.96}=286.6022$$
となります。実際にはICAOでは国際標準大気の気体定数として、より厳密に決定された287.05287を採用しています。
標準大気の大気圧
標準大気に関するこれだけの定義でかなりのことが分かります。今から調べていきましょう。しかし、数学Ⅲで習う積分がどうしても必要になります。ごめんなさい。
まず高度を\(h\)で表します。すると大気圧は\(p(h)\)と表すことができます。次に大気の中の以下のような円柱を考えて、そのつり合いの式を作ります。
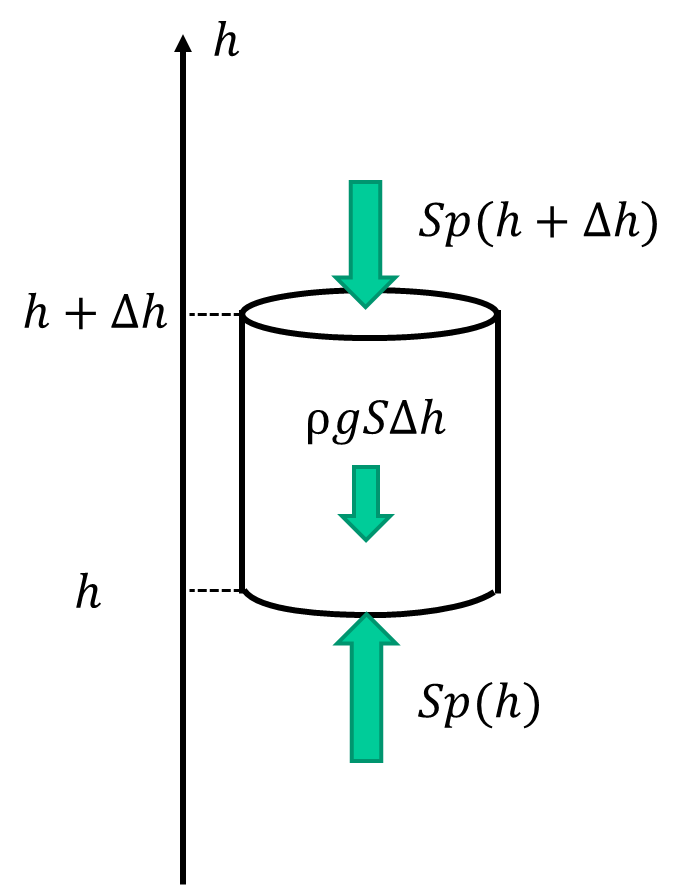
大気は下面から\(Sp(h)\)の力を受け、上面から\(Sp(h+\Delta h)\)の力を受けます。また重力は下向きに、\(\rho g S\Delta h\)となります。よってつり合いの式は、
$$Sp(h)-Sp(h+\Delta h)-\rho gS\Delta h=0$$
となります。ここで、\(p(h+\Delta h)-p(h)=\Delta p\)であるので、次のように書き直すことができます。
$$ \Delta p=-\rho gS\Delta h$$
ここで高度が11000m以下の場合は、温度は高度の関数で\(T=288.15-0.0065h\)と表すことができました。この式と状態方程式\(p=\rho RT\)と合わせて、
$$p=\rho R(288.15-0.0065h)$$
が得られます。この式とつり合いの式から、
$$\frac{\Delta p}{p}=\frac{-gΔh}{R(288.15-0.0065h)}$$
が得られるので、この式を、\(\Delta p\longrightarrow dp、 \Delta h\longrightarrow dh\)と置き換えて両辺を積分すると、
$$\log p=\frac{g}{0.0065R}\log (288.15-0.0065h) +\log C$$
となります。ここで次の計算を容易にするために、積分定数 \(C’\) を \(C’=\log C\) と置いています。
さらに、この式を\(p\)で解くと、
$$p=C(288.15-0.0065h)^{\frac{g}{0.0065R}}=C(288.15-0.0065h)^{5.25}$$
が得られます。
ここで、\(h=0\)のとき、\(p(0)=101,325\)であることに注意すると、
$$101,325=C288.15^{5.25} より C=\frac{101,325}{288.15^{5.25}}$$
となるため、大気圧は高度の関数として、
$$p=101,325×\left(\frac{288.15-0.0065h}{288.15}\right)^{5.25}$$
と表されることが分かります。
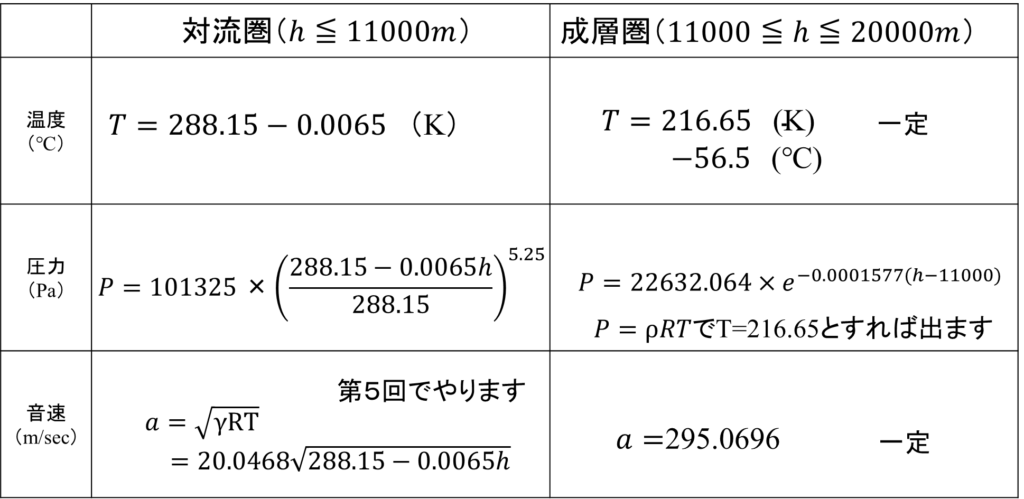
標準大気から分かること
これらの結果をまとめると次のようになります。成層圏の圧力の式は、T=216.65を使うことで、今回の式と同様に求めることができます。突然音速の式が出てきましたが、この式の導出は、第5回の補講で求めます。
第4節 演習問題(標準大気の計算(その1))
標準大気を計算する式が得られたので、実際に計算してみたいと思います。この計算は今後の航空機の計算に必要な計算になります。もちろん、こんな面倒な計算は手で行う必要はないので、MS Excelを使って計算しましょう。
練習問題1 高度5000mでの気圧、気温、密度、音速を計算してみよう
練習問題2 高度15000mでの気圧、気温、密度、音速を計算してみよう
①以下のように高度の入力欄を作成します。

②B2セルに、気圧の式を入力して気圧を計算します。
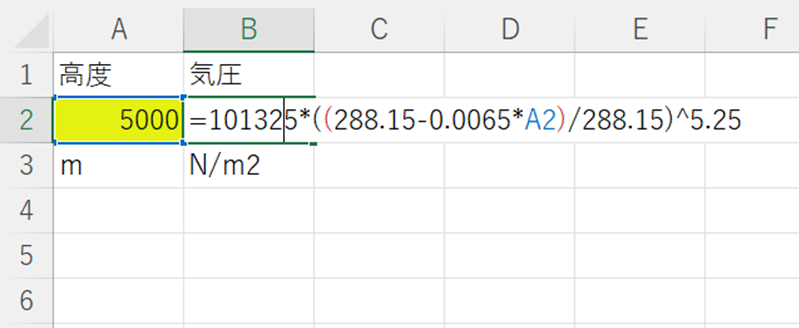
③C2セルに、気温の式を入力して気温を計算します。
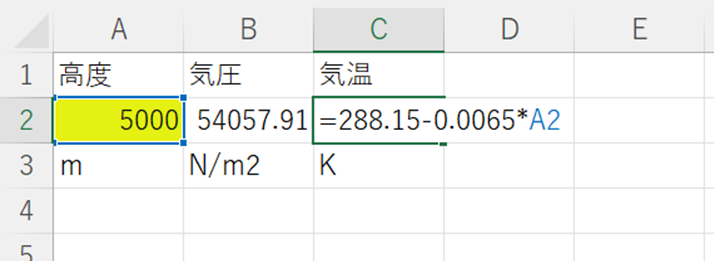
④状態方程式から、\(\rho=p/RT\)をD2セルに入力します。
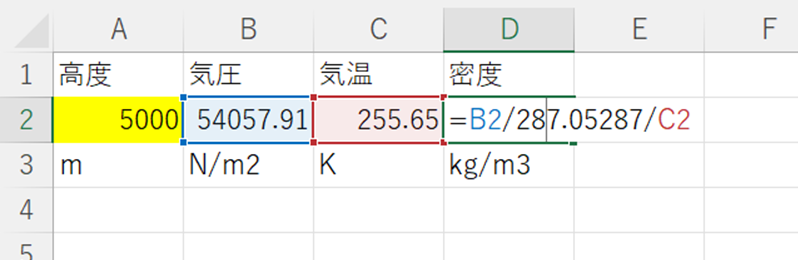
④ 音速の式、\(a=\sqrt(\gamma RT)\)をE2セルに入力します。(\(\gamma\)は空気の比熱比1.4を用います。)
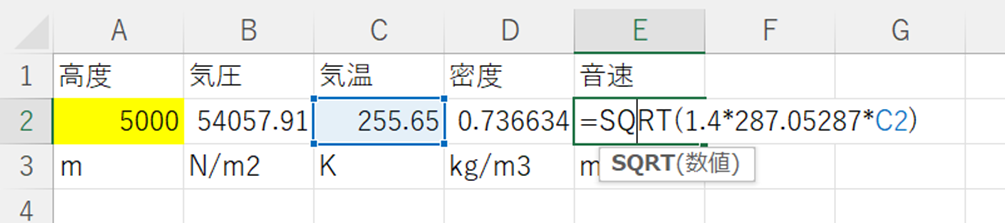
以上で、練習問題①は終了です。A1セルの値を変更すれば、11000m以下の値であればどんな高度でも計算できるようになっています。
一方で、高度11000m以上の場合は、式が変わってしまうので、式を入力し直す必要があります。高度に合わせて式を入力し直すのは大変ですので、どちらも計算できるように条件関数「 IF 」を使って入力していきます。
①B2セルを次のように修正します。

②C2セルを次のように修正します。
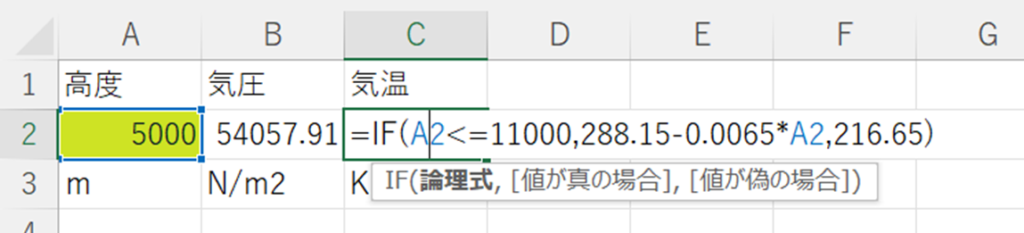
以上で完成です。密度と音速はB2セルとC2セルの値で決まるので、修正する必要はありません。これで、どんな高度でも標準大気の状態を知ることができるようになりました。
第5節 演習問題(標準大気の計算(その2))
本航空工学講座では、MS Excelの力を借りて様々な計算を行います。Excelの練習もかねて、もう少しエクセルの練習をしていきましょう。
練習問題3 縦軸高度 横軸気圧のグラフを描こう
1 まず計算するシートを準備します。
①A2セルに0を入力します。
②A3セルに「=A2+1000」を入力します。
③A3セルをコピーして、A4セルからA13セルに貼り付けます。
※A3セルの「A2+1000」を張り付けたA4セルは、数式が上手くずれて「A3+1000」と入力されています。これはA3セルから見たA2セルの位置関係(A2セルはA3セルの1つ上)を保持するように、A数式が4セルにコピーされたため、数式が同じ位置関係を保つように自動的に修正されたからです。このようなセルの参照方法を相対参照といい、エクセルを活用するためには、必要不可欠な参照方法になります。一方で、コピーする場合にセルを動かしたくない場合もあります。その場合は、数式内で「$A$2」のように「$」を付けて参照します。この参照方法を絶対参照と呼び、こちらも必要不可欠な手法です。詳しくはM&S講座 第1章 エクセルの準備を確認してください。

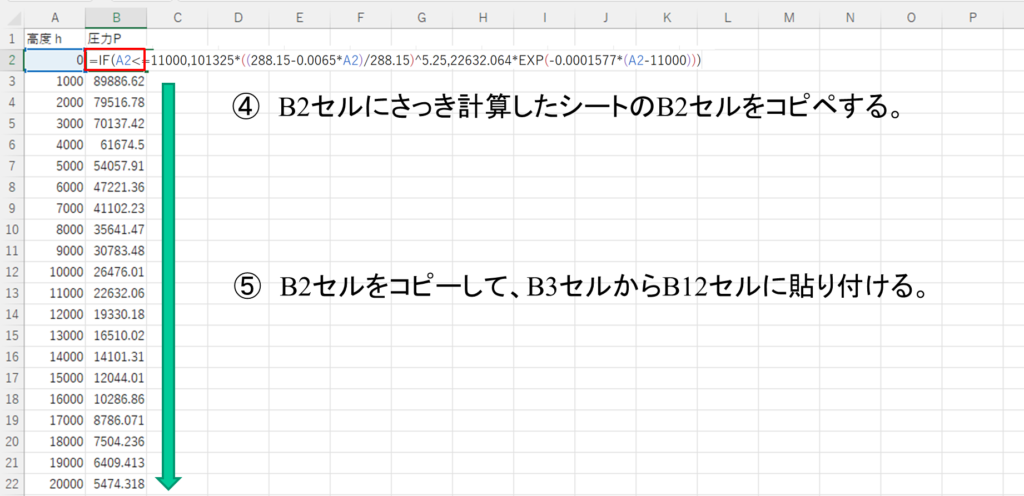
2 各高度の大気圧を計算しま\す。
④B2セルにさっき計算したシートのB2セルをコピペします。(入力しても構いません)
⑤B2セルをコピーして、B3セルからB12セルに貼り付けます。
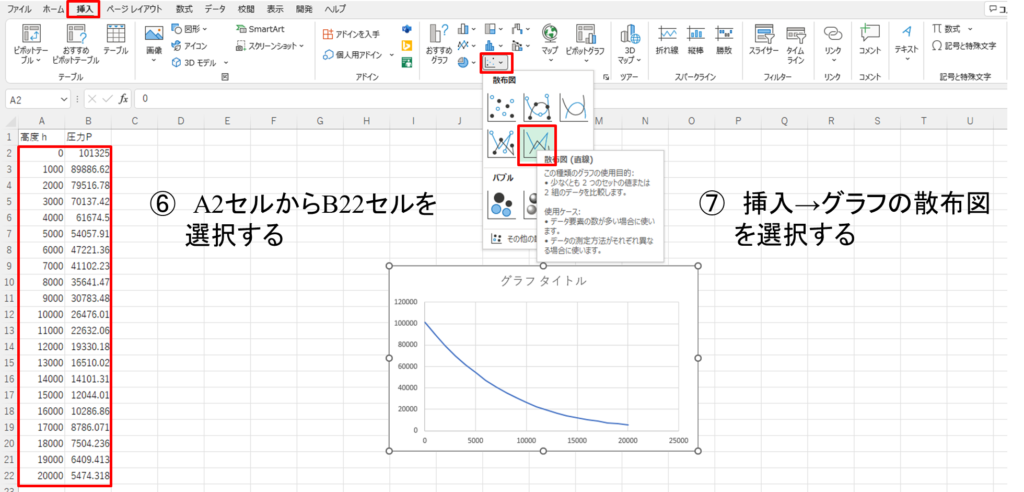
3 計算結果をグラフに出力します。
⑥A2セルからB22セルを選択します。
⑦挿入→グラフ→散布図を選択すると、グラフが出力されます。
4 グラフのx軸とy軸を入れ替えてグラフを修正します。
⑧グラフを選択すると、データの範囲が表示されます。
⑨データの範囲を移動します。
⑩データの範囲を入れ替えます。
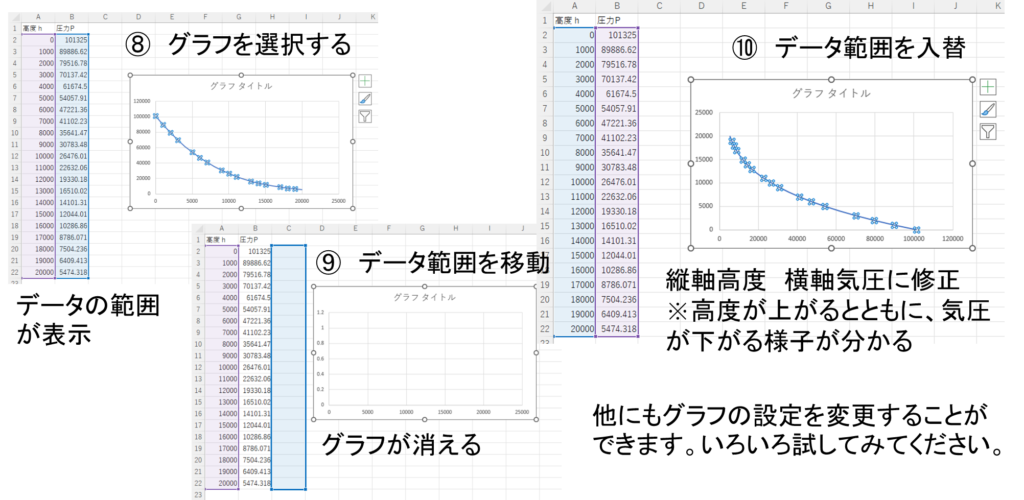
以上で、グラフが完成します。
同じ要領で、以下のとおりグラフを描いてみてください。
練習問題4 縦軸高度 横軸気温のグラフを描こう
練習問題5 縦軸高度 横軸音速のグラフを描こう
練習問題6 縦軸高度 横軸気圧のグラフを、100mごとの高度で描こう
