第1節 迎角(AOA)
先の章では飛行状態とあいまいな表現で説明をとどめましたが、飛行状態を表す重要なパラメータの1つが迎角\(\alpha\)です。迎角とはAOA(Angle of Attack)と呼ぶこともあり、機体軸(航空機の設計時に決められた向き)と速度の向き(大気中の飛行方向)のなす角を指し、\(\alpha\)により表します。迎角\(\alpha\)は航空工学で非常に重要な変数です。
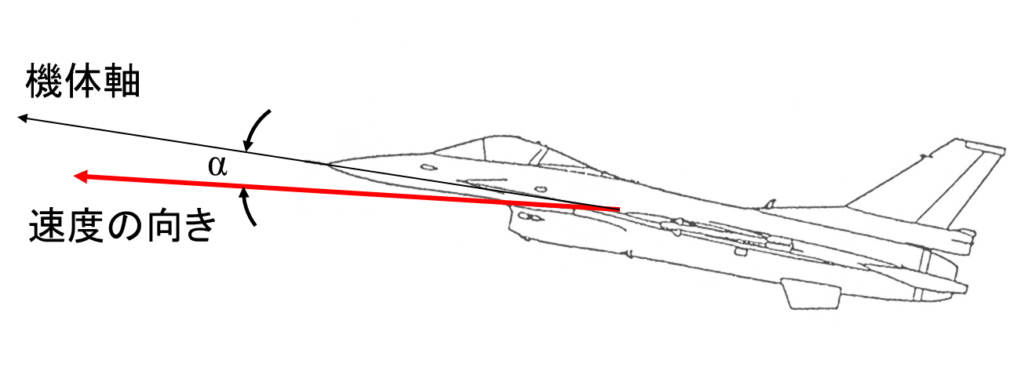
迎角\(\alpha\)は、飛行状態を表すパラメーターになるため、空力係数\(C_{L}\)、\(C_{D}\) は、航空機の形状と迎角\(\alpha\)、レイノルズ数\(Re\)で決まることになります。他に横滑り角\(\beta\)というパラメータもありますが、今回は省略します。
第2節 揚力係数 \(C_{L}\) の性質
空力係数のうち揚力による空力係数\(C_{L}\)を揚力係数と呼びます。この節では揚力係数\(C_{L}\)の一般的な性質を見ていきます。\(C_{L}\)は次のグラフのように表されます。
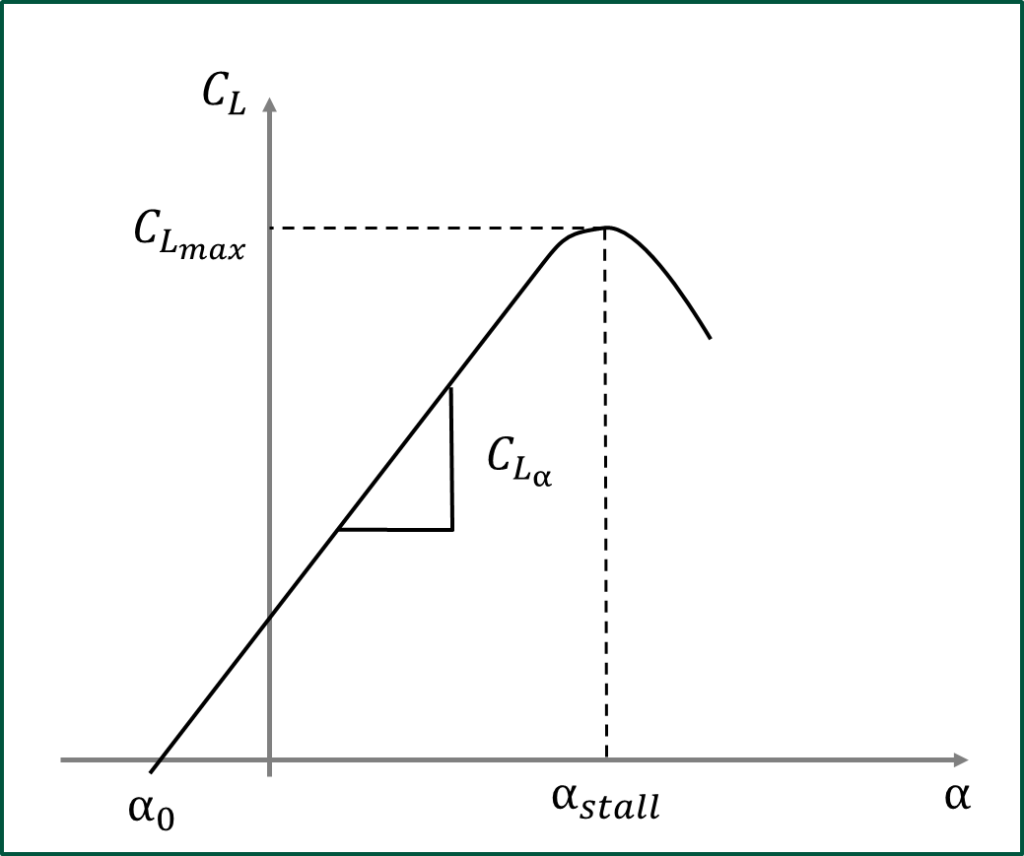
揚力係数\(C_{L}\)の最大の特徴は、\(\alpha\)が小さいときは、直線で表されることです。その直線の傾きを揚力勾配係数と呼び\(C_{L_{\alpha}}\)と書きます。また\(C_{L}\)がゼロになる迎角を\(\alpha_{0}\)と書くと\(C_{L}\)は次のように表されます。
$$C_{L}=C_{L_{\alpha}}(\alpha-\alpha_{0})$$
また\(C_{L}\)には最大値があり、最大値を最大揚力係数、その時の迎角を失速迎角と呼び、それぞれ\(C_{L_{max}}\)、\(\alpha_{stall}\)と書きます。失速迎角\(\alpha_{stall}\)は、飛行安全にもかかわるとても大事な数字になります。
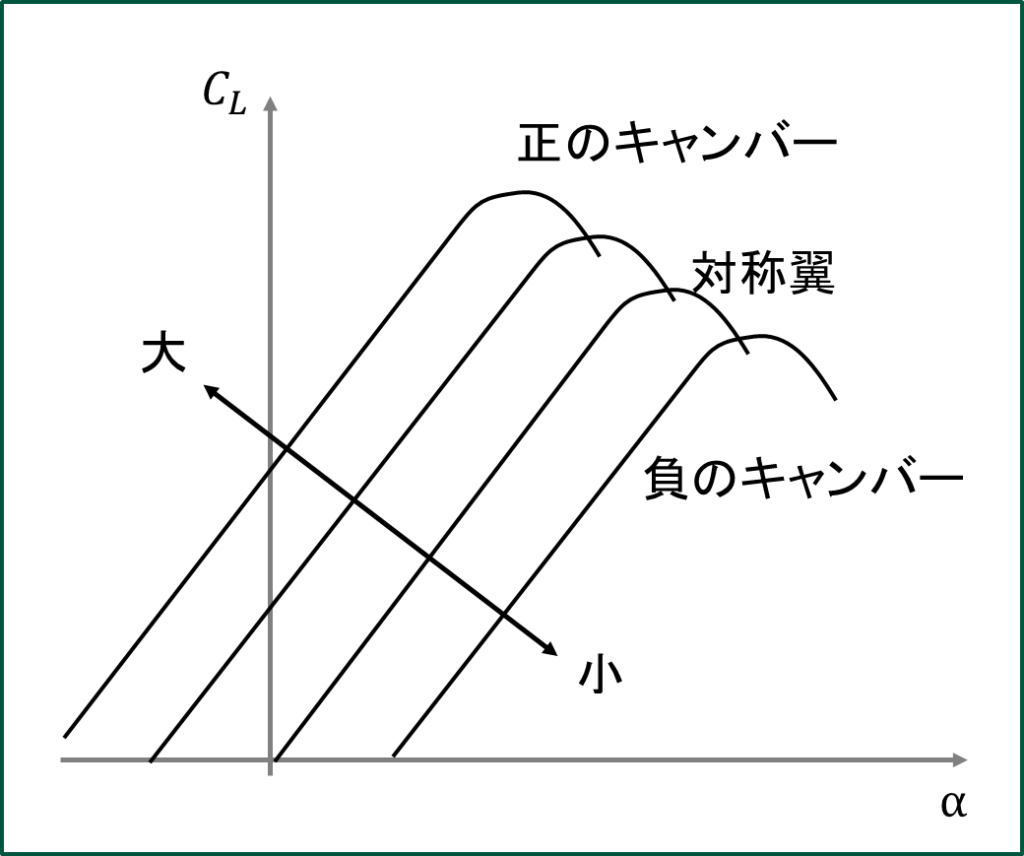
次にキャンバーが与える影響についてみていきます。キャンバーとは翼の中心翼線と翼弦線の離れ具合、つまり翼がどれだけ反っているかを表したものです。キャンバーにはキャンバーがない上下に対称な翼や、反対に沿った負のキャンバーを持った翼も考えることができます。
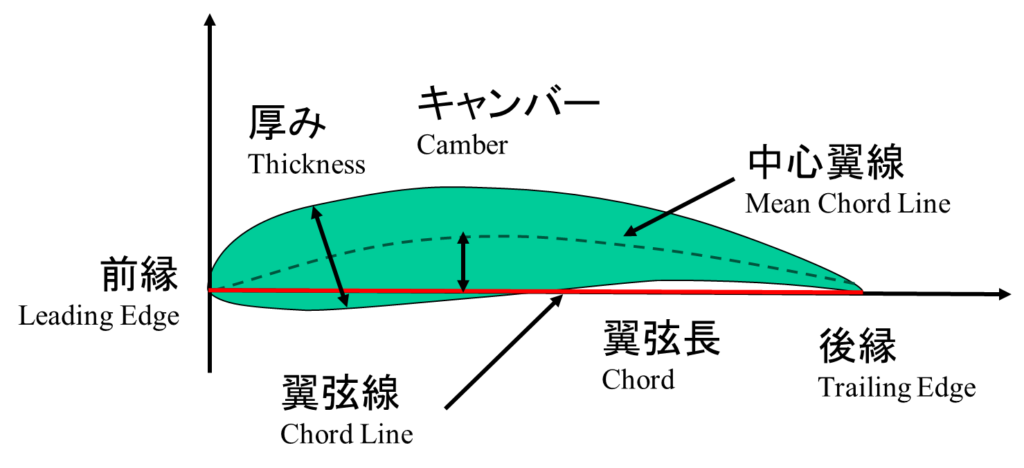
キャンバーを変化させたときに、\(C_{L}\)がどのように変化するかをまとめたのが、次の表になります。大事なポイントは、揚力勾配係数つまり揚力曲線の傾きは同じということです。つまり、キャンバーを変化させても、最大勾配係数は変わりません。一方で最大揚力係数や、失速迎角は変化しています。一般的にキャンバーを大きくすると失速しにくくなります。
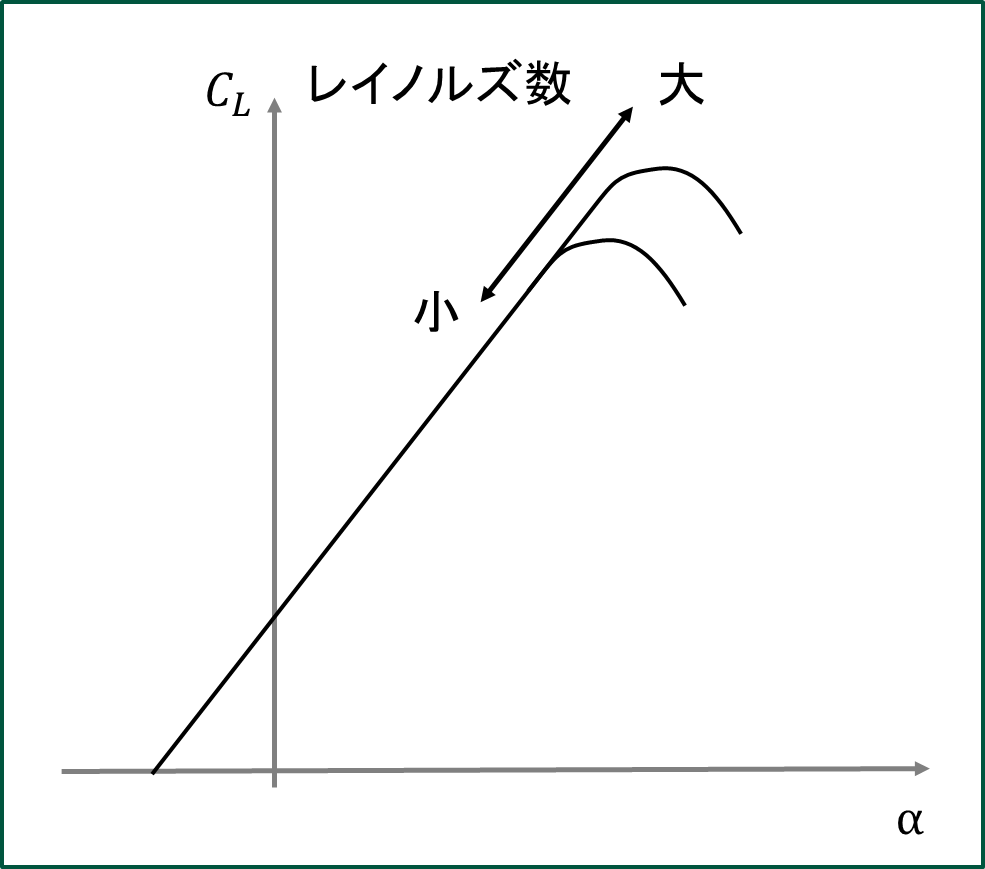
次にレイノルズ数を変化させたときに、\(C_{L}\)がどのように変化するかを表したものが下のグラフになります。レイノルズ数を大きくすると、失速しにくくなります。これは境界層が乱流境界層になるため、流れがはがれにくくなるからです。
また、レイノルズ数を変化させても失速迎角よりも小さい迎角では大きな変化は認められません。このことは、風洞模型で揚力係数を求めた場合に、失速迎角よりも小さい迎角では、大きな差は生じないことを示しています。
揚力係数\(C_{L}\)には、以上のような性質がありますが、実際のデータで確認してみたいと思います。次のデータは実際のデータになります。いろいろなデータが記載されていますが、赤で示した曲線が揚力曲線になります。(機体を含めたデータで使えるものが見つからないため、このデータは翼だけ(胴や垂直尾翼等は含まない)のデータです。)
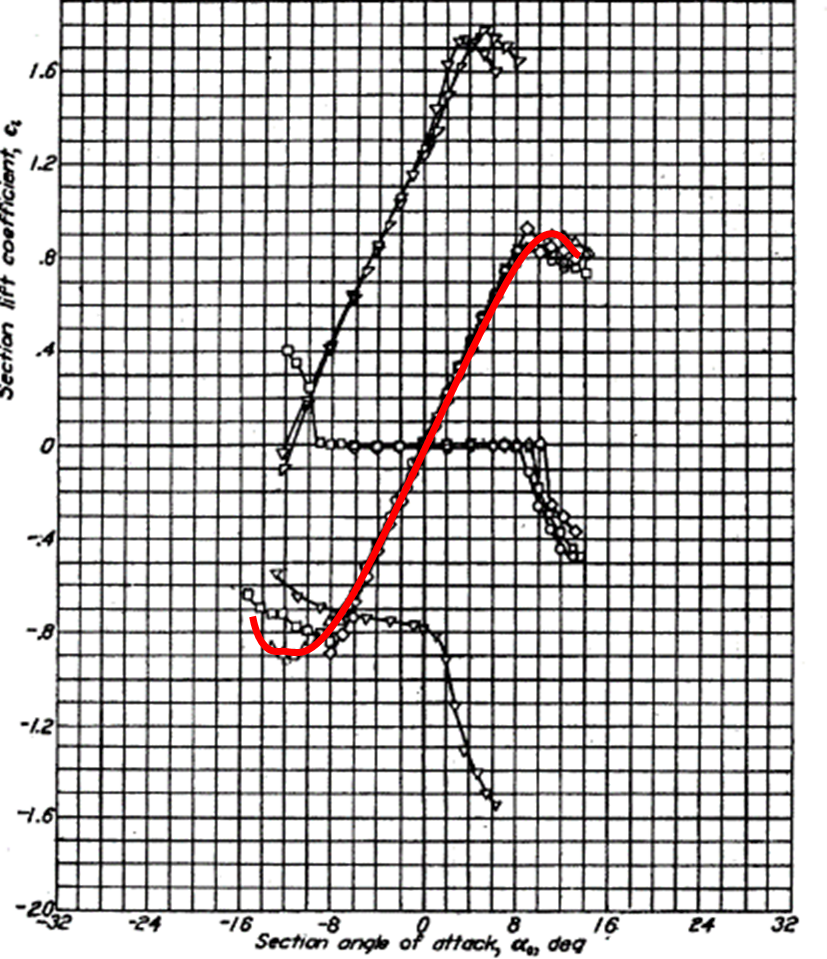
この曲線は迎角が小さい場合は直線で近似することが可能でありその傾きは0.1 1/degとなっています。つまり揚力曲線は
$$C_{L}=0.1\alpha$$
で与えられます。
また迎角が12degを超えると、揚力係数は減少に転じることから失速迎角は12degであり、最大揚力係数は0.9であることが読み取れます。
第3節 抗力係数 \(C_{D}\) の性質
次に、空力係数\(C_{D}\)の性質についてみていきましょう。揚力係数と同様に\(C_{D}\)を抗力係数と呼びます。\(C_{D}\)は一般的に次のグラフのように表されます。
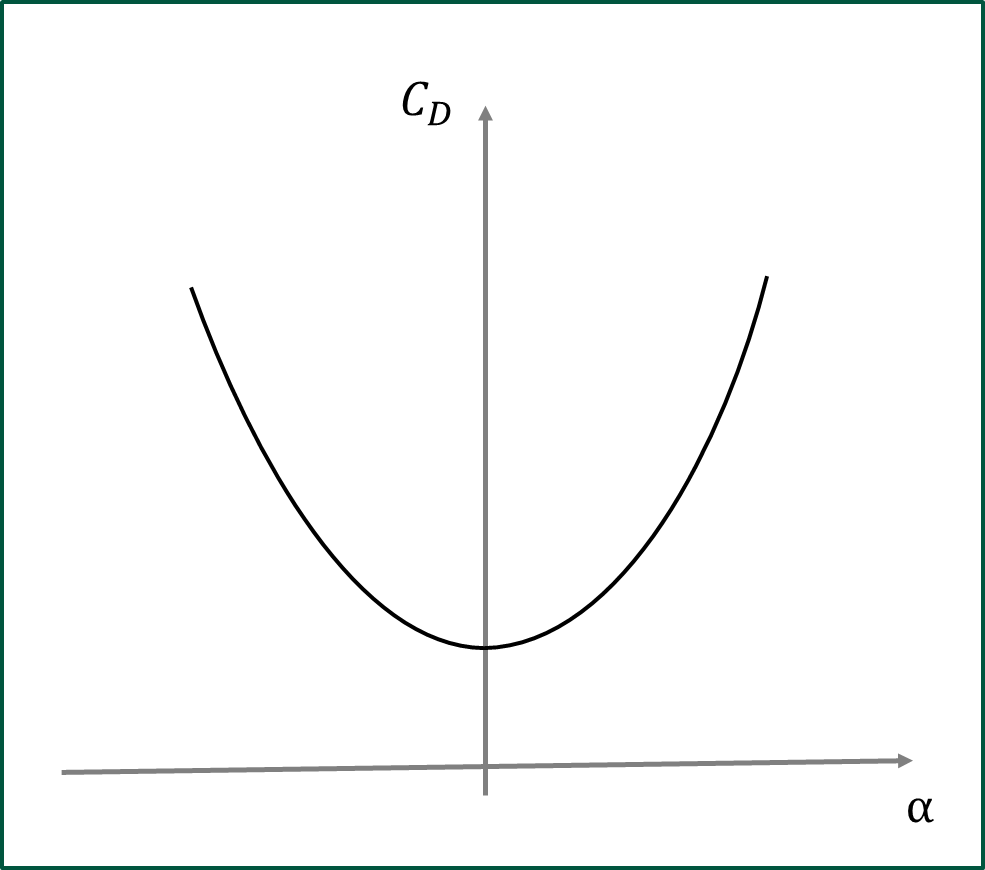
そして、迎角\(\alpha\)が小さいとき、抗力係数と揚力係数の間には次の関係が成り立つことが知られています。
$$C_{D}=C_{D_{0}}+kC_{L}^2$$
つまり、抗力係数は揚力係数の2次関数で表されるのです。この式において、揚力によらない抗力\(C_{D_{0}}\)を有害抗力と呼びます。この有害抗力は、先の章で説明した表面摩擦抗力と圧力抗力に分られます。
また揚力に起因する抗力\(kC_{L}^2\)を誘導抗力と呼びます。この抗力は揚力を発生させるためには必要な抗力になります。この誘導抗力についてもう少し詳しく見ていくことにしましょう。
誘導抗力の比例定数\(k\)は、次のように表されることが知られています。
$$k=\frac{1}{\pi AR e}$$
ここで、 \(\pi\)は円周率、\(AR\)はアスペクト比、\(e\)はオズワルド係数といわれる値になります。円周率はよく知られた値ですが、アスペクト比と\(AR\)とオズワルド係数\(e\)について簡単に説明します。
アスペクト比は縦横比ともいわれる値です。次のような航空機を考えた場合、\(AR=\frac{b}{a}\)となります。このように定義してもいいのですが、航空機の翼は長方形とは限らないため、次のように変形して、翼面積\(S\)を使って次のように定義します。

$$AR=\frac{b}{a}=\frac{b^2}{ab}=\frac{b^2}{S}$$
これらの定義からもわかる通り、翼幅が翼弦に比べて大きい航空機は、大きな\(AR\)を持った機体であると言うことができます。以下のグライダーのような航空機が、高AR航空機の例として挙げることができます。また誘導抗力の定義の式からもわかるとおり、\(AR\)が大きい場合は、誘導抗力は小さくなります。

オズワルド係数\(e\)も\(AR\)と同様に大きければ大きいほど有害抗力は小さくなります。一般的な翼型の場合、この値は0.7~0.9の値をとることが知られていますが、翼型が楕円形の時に最大値1となることが、数学を利用した解析から分かっています。
このことは第二次世界大戦のころには知られていたため、当時の戦闘機に楕円形の翼型をしたものが多く見られます。一方で完全に楕円形をした翼型を作ることで生産性が下がってしまい、それに見合った効果も得られていないことから、現在では楕円形に近い形の翼型が多く採用されています。

空力係数\(C_{D}\)にも、以上のような性質がありますが、\(C_{D}\)についても実際のデータで確認していきます。次のデータは揚力係数で用いたデータと同じ翼のデータになります。いろいろなデータが記載されていますが、赤で示した曲線と青で示した曲線が抗力曲線(横軸は揚力)になります。
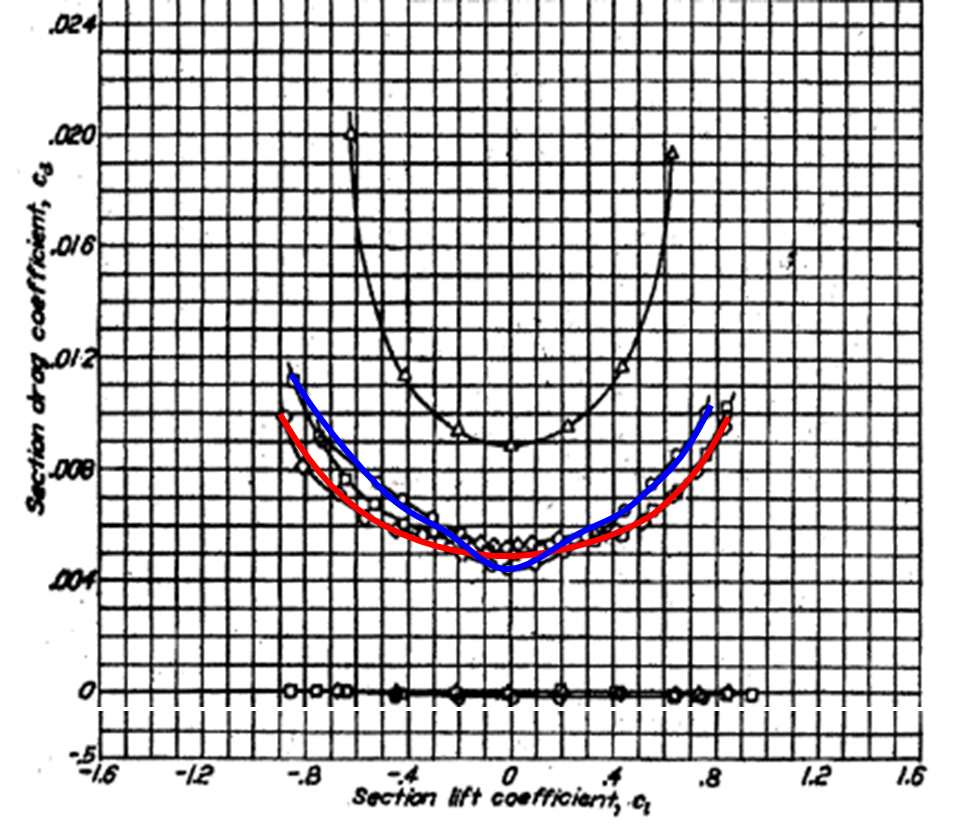
赤い曲線いついて考えてみます、この直線は\((0, 0.05)\)と\((0.8, 0.09)\)を通っていることから、\(C_{L}\)が小さいときは、次のように近似することができます。
$$C_{D}=0.05+\frac{0.04}{0.8^2}C_{L}^2$$
なお、\(C_{L}\)の考察から、\(C_{L}≒0.1α\)と表すことができたので、これを代入すると$$C_{D}=0.05+0.04/8^2 \alpha^2$$
を得ることができます。つまり、抗力は\(\alpha\)が大きくないときは、\(\alpha\)の2次関数でも表すことができるのです。
このグラフには、青い曲線も抗力曲線として記載されています。この曲線は全体的に赤い曲線に比べて大きな抗力を有していますが、揚力が小さいとき、つまり迎角\(\alpha\)が小さいときは、赤い曲線よりも小さい抗力となっています。
これについてはレイノルズ数を用いて次のように説明できます。まず迎角が低い状態では、層流境界層が形成され、表面摩擦力が小さくなります。また後縁部での顕著な剥離もないため、圧力抗力の増大も抑えられているので、有害抗力は小さな値を示しています。
一方で、迎角が大きくなると付近では層流境界層が剥離してしまうため、圧力抗力が増大します。このため、赤い曲線に比べて有害抗力が増大して、全体の抗力を大きくしてしまっているのです。
このような特性は民間機ではよいのですが、軍用機のように多様な速度帯で性能を発揮しなければならない航空機では、あまり好ましくない特性にもなります。そのような場合には、翼面上にこのような突起を取り付けることがあります。(wikipediaより)この突起はヴォルテックスジェネレーターと呼ばれるものであり、境界層をかき乱すことで乱流境界層を作り、剥離を抑えて圧力抗力の増大を小さくすることを目的として取り付けられています。

第4節 演習問題(飛行可能の判定)
空力係数が次の特性を持つ航空機が飛行可能な領域について考えてみます。

$$\begin{align}C_{L}&=\frac{1}{16}\alpha\\C_{D}&=0.5+0.2C_{L}^2\end{align}$$
また、この航空機のデータは以下の通りとします。
翼面積:22.44㎡
重 量:2,421 kg
推 力:100000N(3000m)
※適当に決めた数字です。
演習問題1 この航空機について「高度3000mで時速540km(150m/sec)で水平飛行できるか?」について調べなさい。
模範解答
計算には各高度の空気の状態が必要なため、第1回で作ったシートを利用します。この高度での空気密度は、A2セルに3000と入力すれば、0.909497kg/m3であることが分かります。
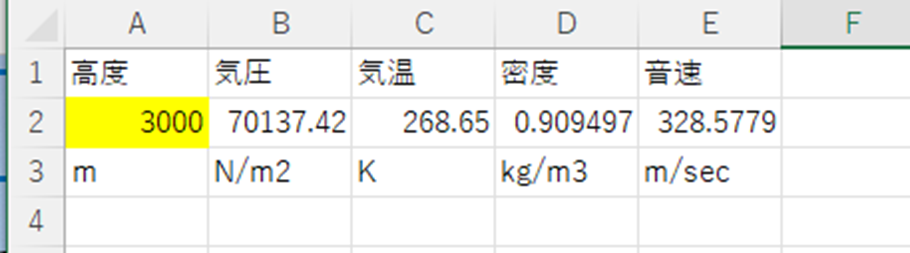
この領域を飛行可能かどうかは、推力と抗力を比較することで判定します。抗力の空力係数を求めるには、そのときの揚力係数が必要になりますが、揚力は実機の重力と釣り合っていることから、重力を揚力とみなして求めることができます。そのためには、新たに7行目に次のように入力して、揚力係数を求めていきましょう。
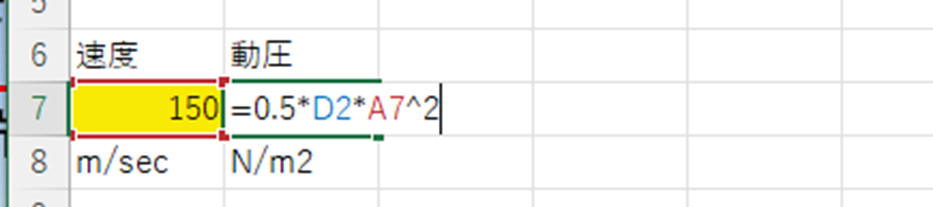
すると、高度3000mを速度150m/secで飛行する航空機の動圧\(q\)は、
$$q=\frac{1}{2}\rho v^2= 10231.84 (𝑁/𝑚^2)$$
となることから、揚力の空力係数は次のように入力すれば求めることかできます。
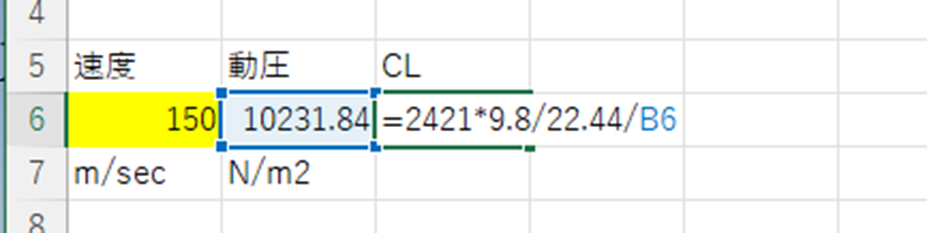
揚力の空力係数が求まれば、抵抗の空力係数は条件の式
$$C_{D}=0.5+0.2C_{L}^2$$
を使って、\(C_{D}=0.502136\)と求めることができます。
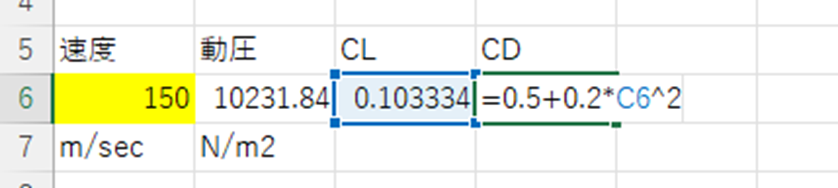
最後に、この値を抗力に戻せばこの飛行状態での抗力を求めることができます。$$D=qSC_{D}$$
であるので、約\(D=115000\)と求めることができます。
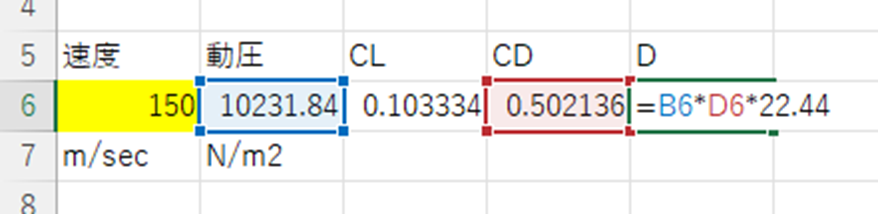
この力はエンジンの推力100000Nよりも大きな値となっているので、この航空機は高度3000mを150m/secで水平飛行できないことが分かります。なおここでいう飛行できないは水平飛行状態を保てないという意味です。より高い高度から降下しながら加速することで、一時的にその飛行状態を達成することは可能です。
演習問題2 この航空機について「高度3000mで時速140km(40m/sec)で水平飛行できるか?」について調べなさい。
模範解答
先ほど作成したエクセルシートは万能なため、速度のA6セルに40と入力すると、必要な推力を計算してくれます。
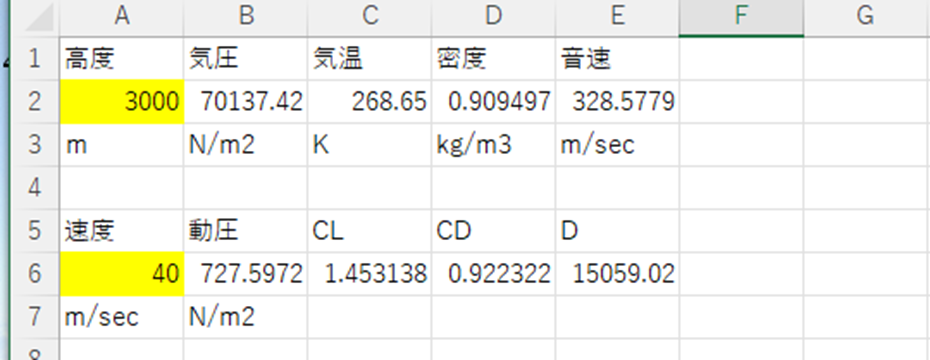
必要な推力は約15000(N)となり、一見飛行できそうです。しかしもう1つの条件を確認する必要があります。
その条件は、迎角\(\alpha\)の条件です。速度が低くなると動圧が低くなるため、空力係数が大きくならなければ飛行できなくなります。しかし空力係数は、失速迎角\(\alpha_{stall}\)で最大\(C_{L_{max}}\)となるため、この値を超えては飛行できなくなります。この値を比較してもいいのですが、失速迎角で比較することが一般的なため、次のように迎角\(\alpha\)を計算してみます。
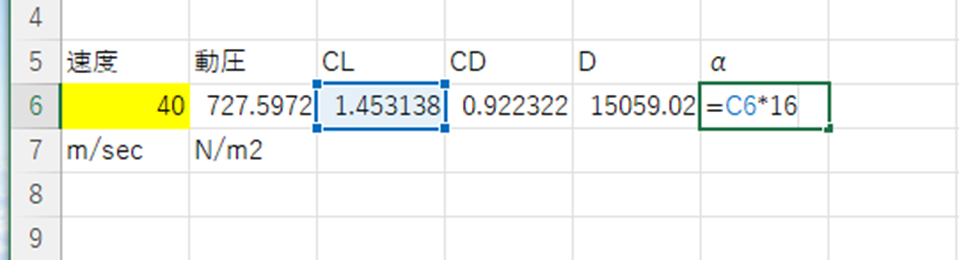
このように迎角を計算すると、\(\alpha=23.3 (deg)\)となり、失速迎角16degを超えます。このため、この航空機は40m/secでは、遅すぎて飛行できないことが分かります。
以上をまとめると、航空機が飛行可能な領域は次のようになります。
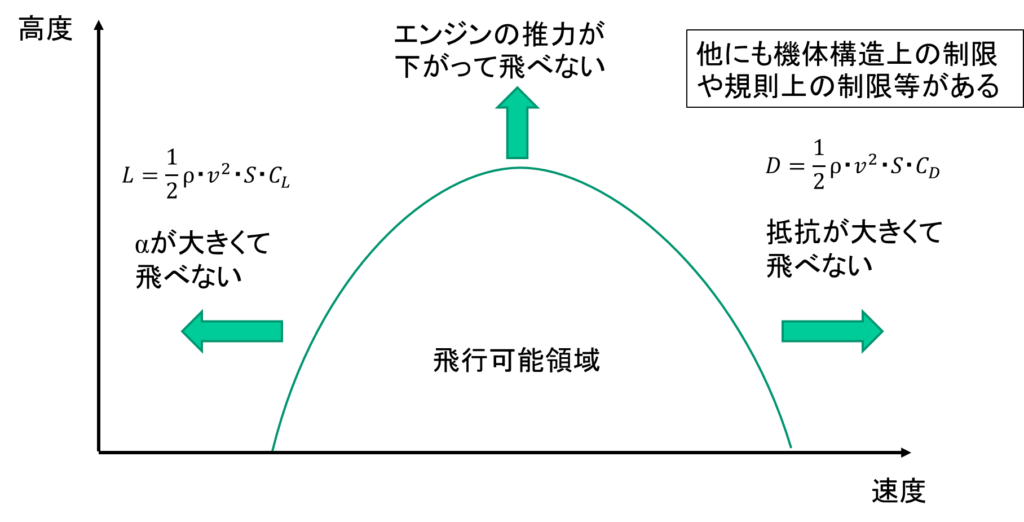
速度が速い領域は、抵抗が大きくなって飛行できない
速度が遅い領域は、迎角が失速迎角を超えてしまい飛行できない
高度が高い領域は、エンジンの推力が下がって飛行できない
※それ以外にも、さまざまな制限があります。
このように航空機が飛行可能な領域を「エンベロープ」と呼びます。
第5節 演習問題(エンベロープを求める)
演習問題3 演習1で用いた航空機について、各高度での推力が以下のとおりの時、各高度と各速度で飛行可能かどうかを判定せよ。
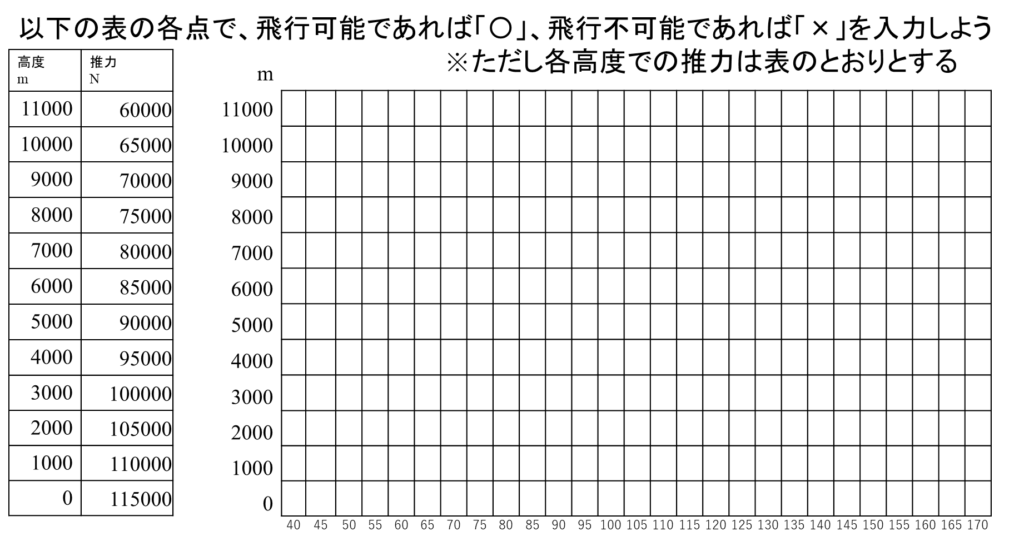
エクセルファイルは次のファイルをダウンロードして利用する。
模範解答
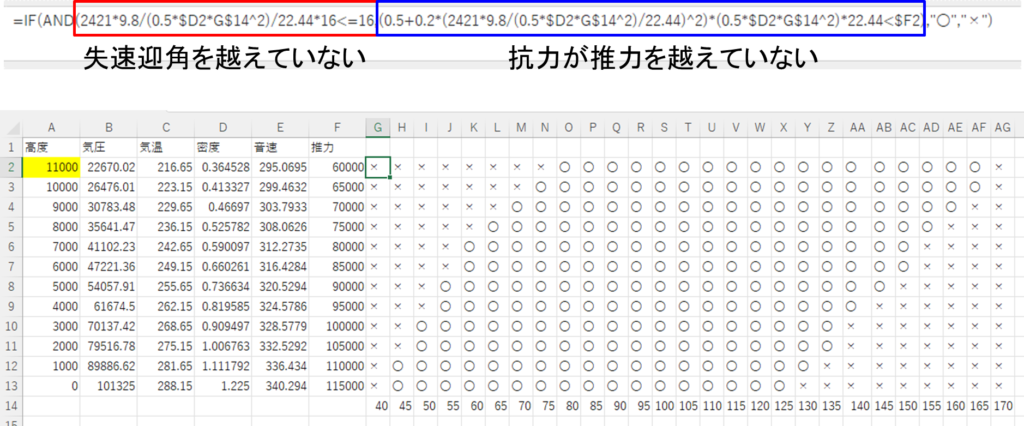
①方針
エクセルファイルをダウンロードすると、次のシートが作成されていることから、各高度と速度毎での抗力と推力の比較および、迎角と失速迎角の比較をそれぞれ行い、飛行可能か同課の判定を行う。
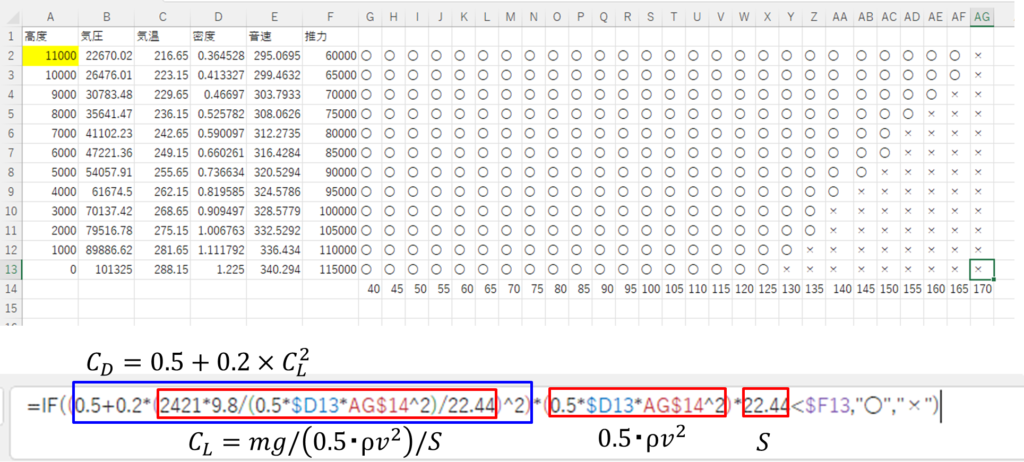
②推力と抗力を比較
AG13セルに次のように入力して、そのAG13セルをG2セルからAG13セルにコピペする。
式の内容については、枠外の式を参考にする。
③迎角と失速迎角を比較
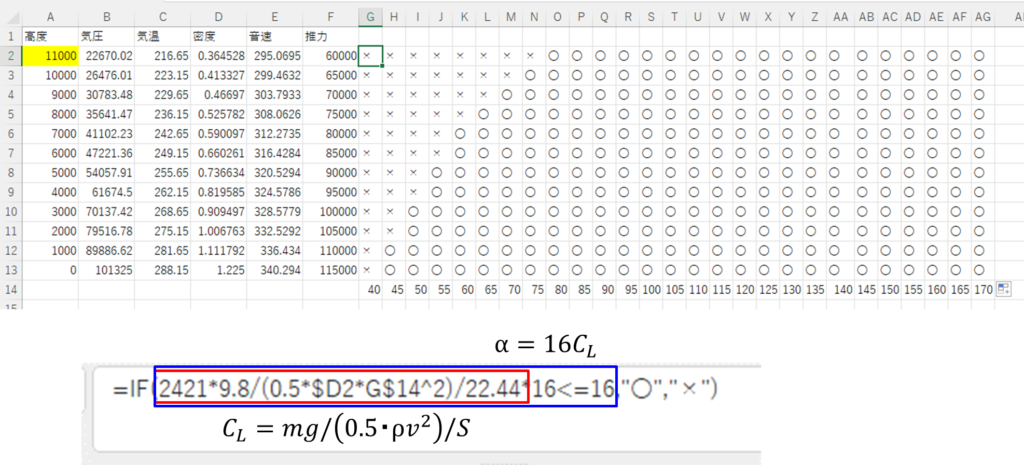
G2セルに次のように入力して、そのG2セルをG2セルからAG13セルにコピペする。
式の内容については、枠外の式を参考にする。
④推力と抗力、および、迎角と失速迎角を同時に比較
G2セルに次のように入力して、そのG2セルをG2セルからAG13セルにコピペする。
式の内容については、枠外の式を参考にする。