M&S講座で扱う最初のモデルとして、今回は数列の考え方を応用して、新型コロナウイルス感染症の時に話題になったSIRモデルを作ってみたいと思います。数列の考え方を使いますが、数列に関する知識はなしで構いません。むしろ無い方がいいかもしれません。
第1節 人口増加モデル
数式モデルの作成
SIRモデルをいきなり扱うのはちょっと難しいので、まずは簡単な人口増加モデルから考えてみたいと思います。
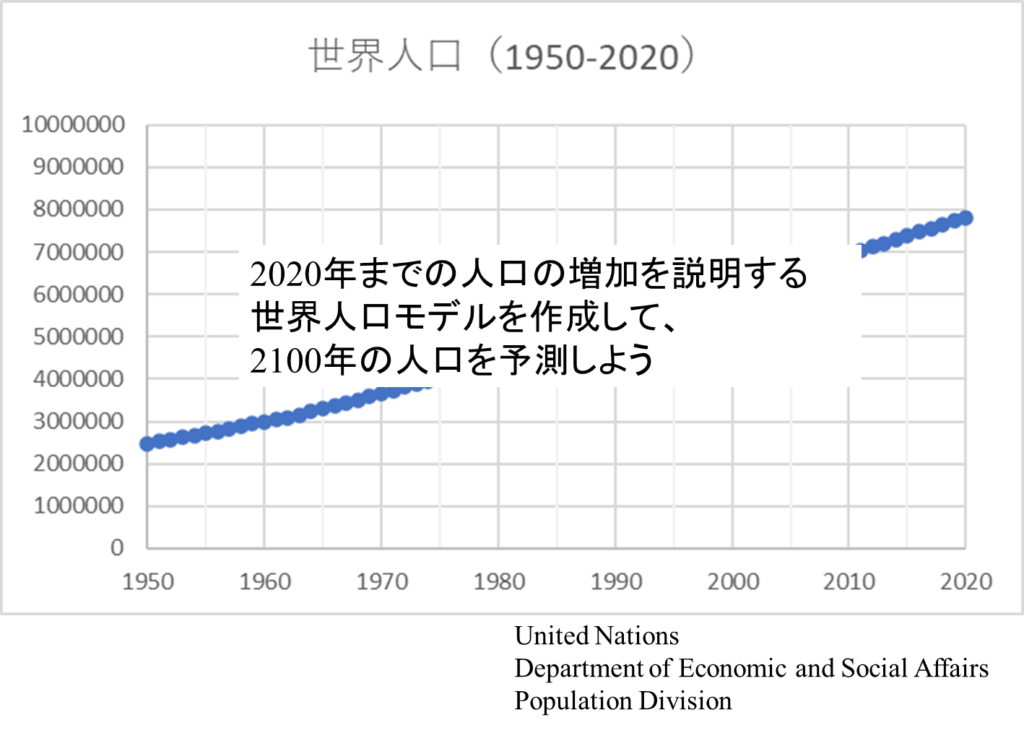
目標は、世界人口の推移データを使用して、次のような世界人口モデルを作成して、2100年の人口を予測したいと思います。
ある年の人口を\(X_{t}\)として、その年に生まれた人口を\(B_{t}\)、その年に亡くなった人口を\(D_{t}\)、翌年の人口を\(X_{t+1}\)とします。
すると次のような関係が成り立ちます。
$$X_{t+1}=X_{t}+B_{t}-D_{t}$$
ここで、次のように考えます。
生まれた人口は、その年の人口に比例する ⇒ \(B_{t}=\alpha X_{t}\)
死亡した人口は、その年の人口に比例する ⇒ \(D_{t}=\beta X_{t}\)
つまり
$$X_{t+1}=X_{t}+B_{t}-D_{t}=X_{t}+\alpha X_{t}-\beta X_{t}=(1+\alpha+\beta)X_{t}=(1+\gamma)X_{t}$$
が成立します。
ここで、\(X_{t+1}=(1+\gamma)X_{t}\) における \(\gamma\)は人口増加率になります。

シミュレーション
ここで得られた式が人口増加モデルの数式モデルになります。では早速この式を使ってシミュレーションをしてみましょう。まずは次のファイルをダウンロードしてください。
すると次のようなシートが現れます。A列には西暦、B列には実際の人口(千人)が入力されています。このC列に、今作った数式モデルのシミュレーション結果を出力してきましょう。
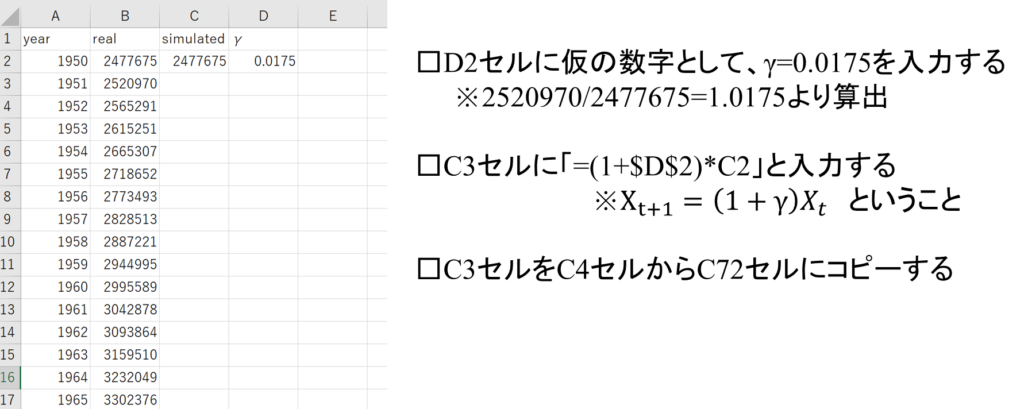
①初期条件を入力する。
・C2セルにB2セルの値(1950年の実データ)をコピペします。
・仮の人口増加率として、D2セルに0.0175を入力します。
※この値は、1951年の人口を1950年の人口で割った値です。
※=B3/B2-1と入力しても構いません。
②数式モデルを入力する。
・C3セルに「=(1+$D$2)*C2」と入力する。
・C3セルをC4セルからC72セルにコピペする。
たったのこれだけでシミュレーションが終わったことが分かるでしょうか?
C3セルには、2477675(千人)を1+0.0175倍された2521034が
C4セルには、2521034(千人)を1+0.0175倍された2565152が
C4セルには、2565152(千人)を1+0.0175倍された2610042が
・・・
がそれぞれ出力されています。要は最初の値を2477675としておき、式\(X_{t+1}=(1+\gamma)X_{t}\)により、次々と次の年の人口を計算したことになります。
この式は数列で習う漸化式の形をしています。数列を習うと漸化式の一般項を求める練習を沢山行いますが、漸化式そのものを、応用する場面はあまり見かけないのではないでしょうか。これが漸化式の一番大事な使い方ではないかと思います。この漸化式なら一般項を簡単に求めることができますが、この話では一般項は本質的ではないので説明はしません。簡単に分かるので、習っている人は求めてみて下さい。
第2節モデルのチューニング
モデルを作ってシミュレーションを行った場合に、シミュレーション結果が実際の減少によく合うように、モデルを見直すことをモデルをチューニングするといいます。ここではモデルをチューニングについてみていきたいと思います。
パラメータの調整
数式モデルのチューニングの基本は、実際のデータに一致するようにパラメータを調整します。一般的に、何らかの誤差が最小になるようにパラメータを調整することが基本ですが、ここではそこまで踏み込まずに、シミュレーション結果がもっともらしいあたりになるまで、トライアンドエラーでパラメーターを変更することとします。
モデルは
$$X_{t+1}=(1+\gamma)X_{t}$$
だったので、パラメータは\(\gamma\)の1つしかないためこの値を変更してもっともらしい結果になるように調整します。そのためには次のようにグラフを作成してから、パラメータを調整をします。
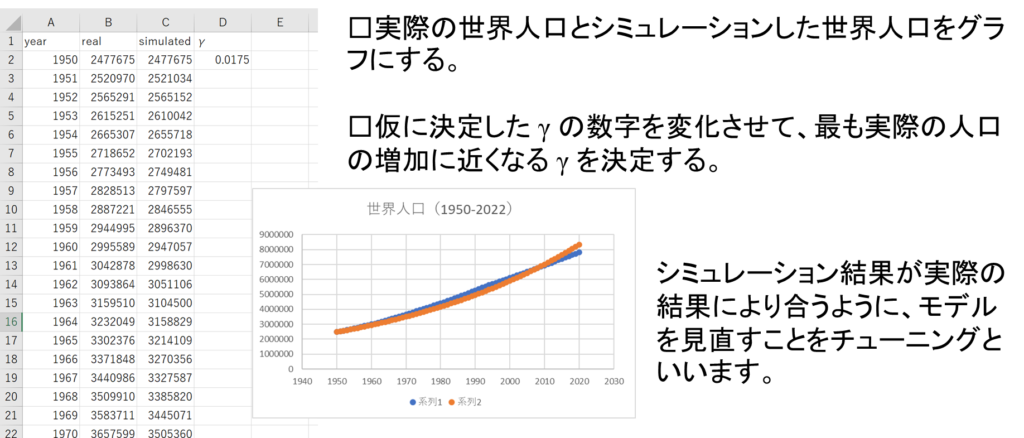
①実データとシミュレーション結果をグラフにする。
・A2セルからC72セルを選択
・挿入→グラフ→散布図からグラフを挿入する。
②パラメータの調整
・D2セルの値を変更して、最も適切な結果になるまでシミュレーションする。
モデルの調整
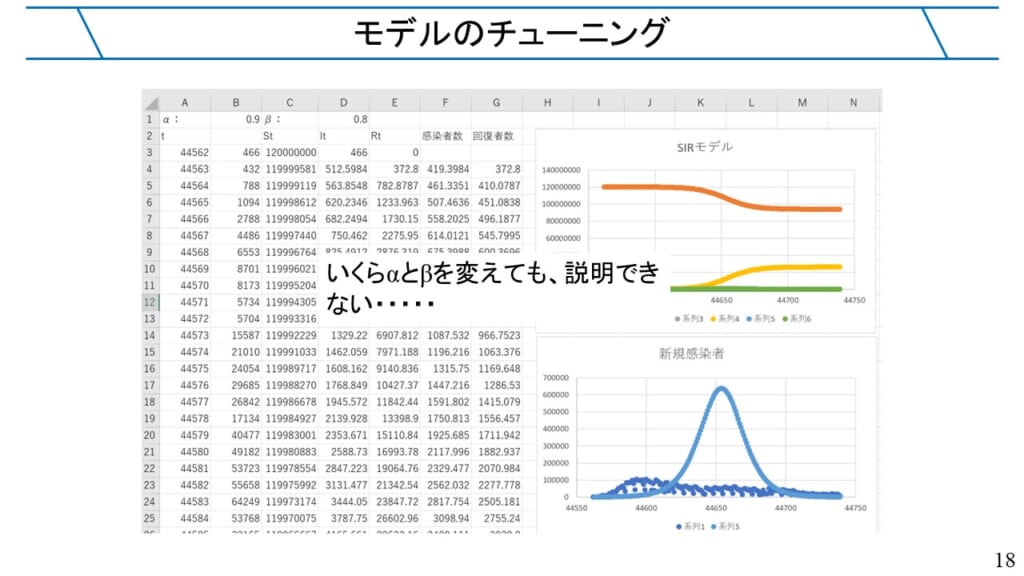
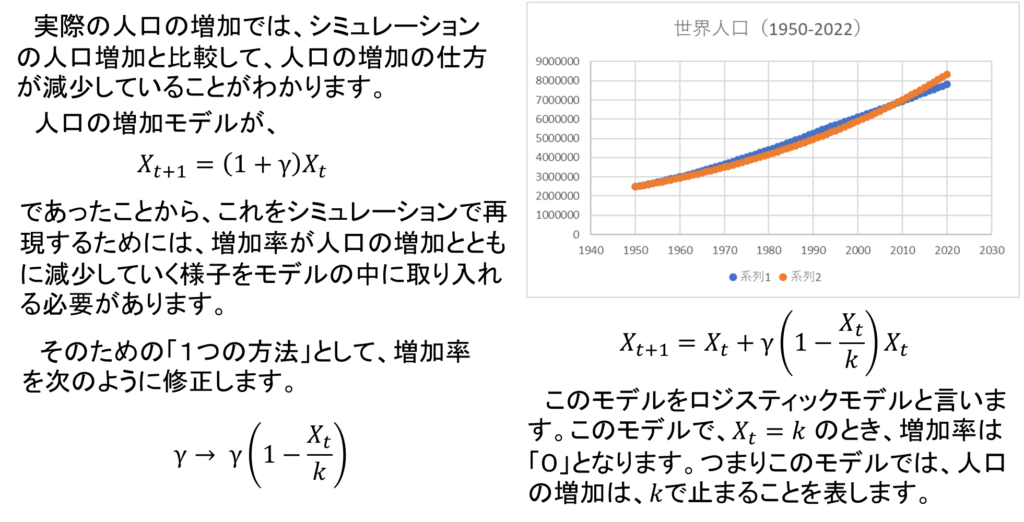
パラメータをいくら調整しても完全に一致させることは難しいことが分かります。特にグラフを比較してみると、実際の人口データが、シミュレーション結果ほど増加していないことによります。つまり、今回採用した数式モデルは人口の増加率が一定と仮定していましたが、実際の人口増加をシミュレーションするためには、人口が増加したときに増加率が低下していくことを数式モデルに反映させる必要がありそうです。つまり、数式モデル自身も調整する必要がありそうです。数式モデルを調整する方法は数多くありますが、今回は次のように考えてみましょう。
人口増加率\(\gamma\)が人口が増加した場合に小さくなるように、\(\gamma\)を次のように置き換えます。
$$\gamma \longrightarrow \gamma\left(1-\frac{X_{t}}{k}\right)$$
つまり次のモデルを考えることになります。
$$X_{t+1}=X_{t}+\gamma\left(1-\frac{X_{t}}{k}\right)X_{t}$$
このモデルにはロジスティックモデルという名前があります。このモデルでは、\(X_{t}=k\)のとき、\(X_{t+1}=X_{t}\)となります。つまり人口増加は\(k\)で止まることを表します。
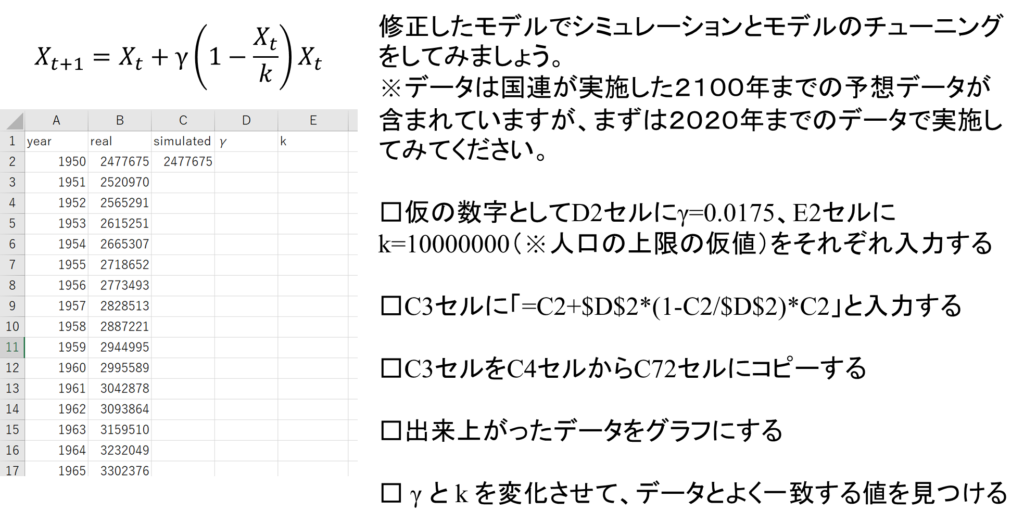
それでは新しく作った数式モデルを使って、「人口増加2」のシートを使ってシミュレーションをしていきましょう。
①パラメータの設定
・C2セルに247675と入力します。
・とりあえず、D2セルに0.0175(\(\gamma\))、E2セルに10000000(\(k\)と入力します。
②数式モデルの入力
・C3セルに、「C2+$D$2*(1-C2/$E$2)*C2」と入力する
・C3セルをC4セルからC72セルにコピーする。
③出来上がったデータをグラフにする。
・A2セルからC72セルを選択する。
・挿入→グラフ→散布図からグラフを挿入する。
④パラメータを調整する。
・D2セルとE2セルの値を変更して、データとよく一致する値を見つける。
シミュレーションを使った未来予想
以上の手法で、人口の増加を表す数式モデルを作成し、その結果が実際の人口データとよく一致するようにチューニングを行いました。このシミュレーションを行う意義は、未来を予測したり、危険性を事前に評価したりすることにあります。人口の増加モデルも数式を先に延ばせば、未来の予測を行うことができます。またデータには、国連が発表した人口予測データも含まれています。
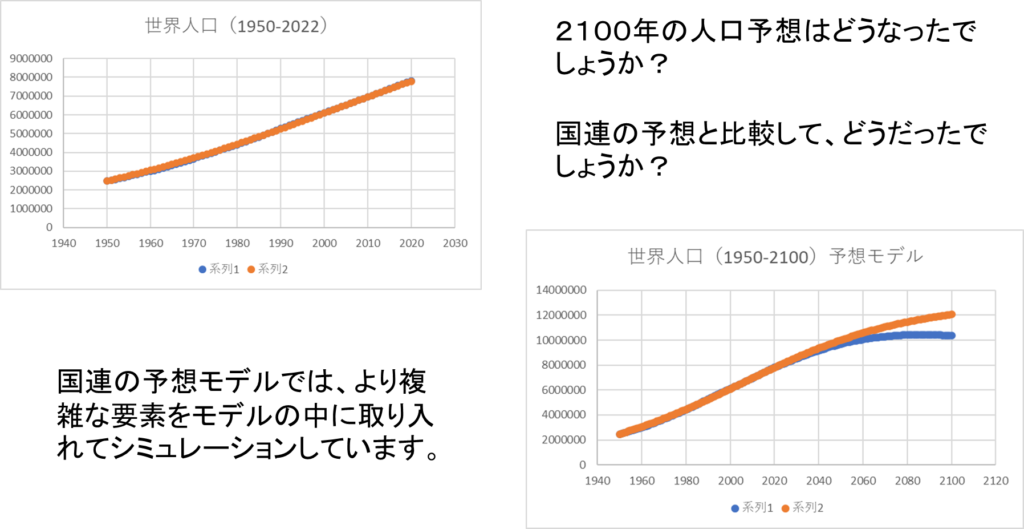
実際に2100年までの人口増加をシミュレーションすると、自分が行ったシミュレーションと国連が発表した人口予測には大きな開きがあるのではないでしょうか。
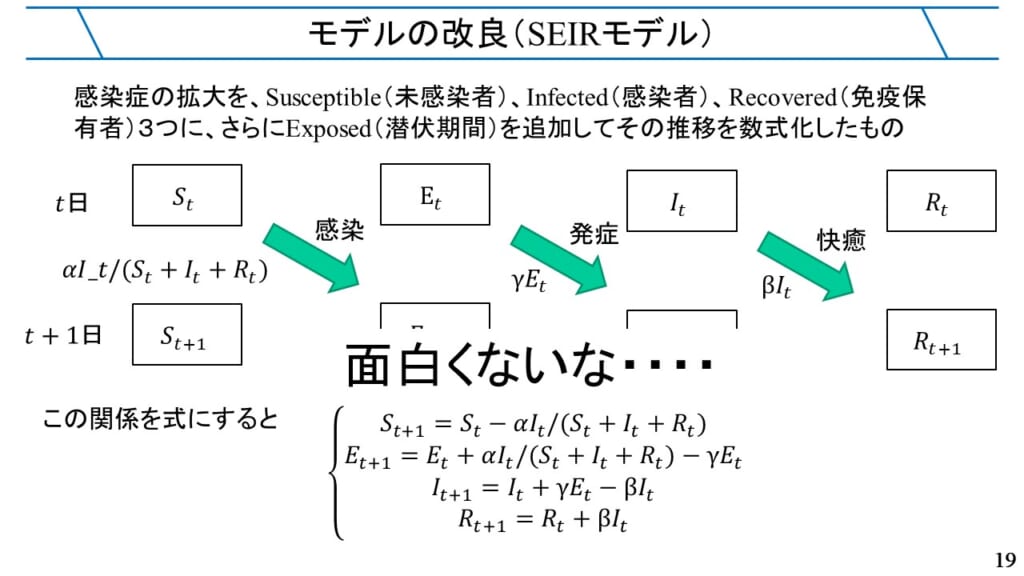
ロジスティックモデルでは、人口が増加すると増加率が低下することだけを再現していましたが、国連のシミュレーションではより複雑な要素をモデルの中に取り入れていてシミュレーションを行っています。しかし、考え方の基本は同じです。人口の増加モデルに関する考察はここで終わりにして、次はより複雑な感染症の拡大を模擬するSIRモデルやその改良モデルについて考察していきましょう。
第3節 SIRモデル
数式モデル
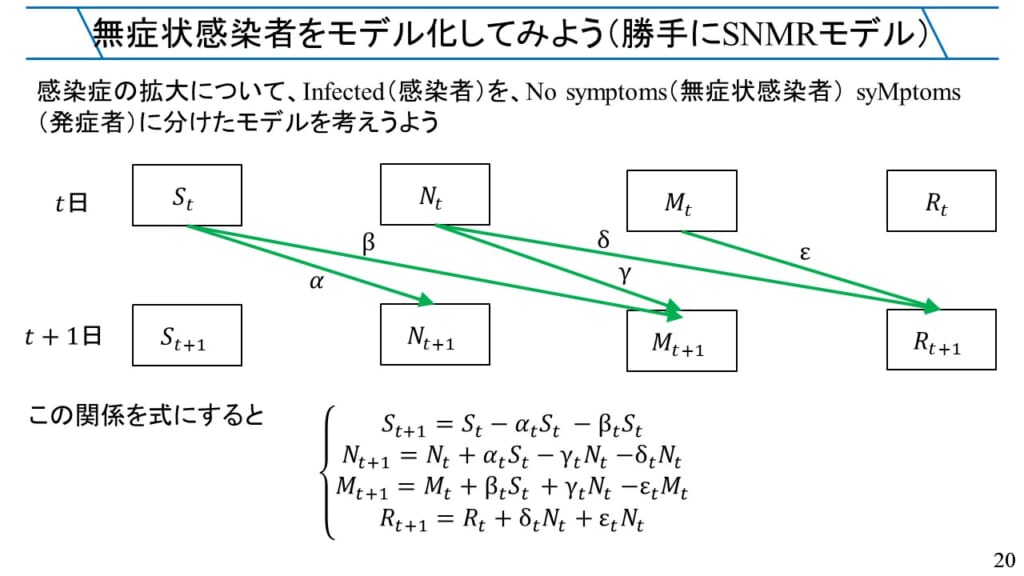
感染症が拡大していく様子をシミュレーションするSIRモデルについて考えていきます。対象となる国や地域などに住む住人は、Susceptible(未感染者)、Infected(感染者)、Recovered(回復者)の3つに分けることができます。ある日\(t\)におけるそれぞれの数を\(S_{t}\)、\(I_{t}\)、\(R_{t}\)とします。すると翌日\(t+!\)の感染者数は、\(S_{t+1}\)、\(I_{t+1}\)、\(R_{t+1}\)となります。
ここで未感染者の一定の割合が感染すると考えると、その割合を感染率\(\alpha\)と呼ぶとすると、\(\alpha S_{t}\)が感染して感染者になります。また、同様に感染者の一定の割合が回復すると考えて、その割合を回復率\(\beta\)と呼ぶとすると、\(\beta I_{t}\)が回復して回復者になります。
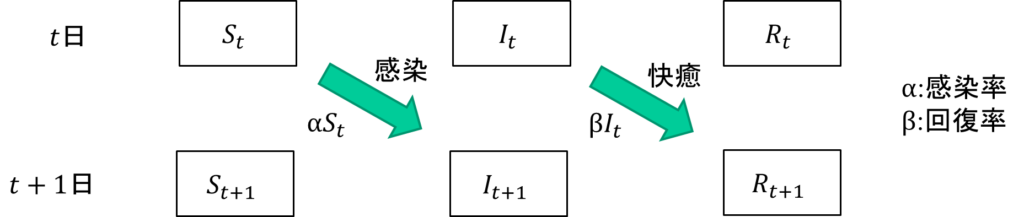
この時を式に表すと次のように表されます。
$$\begin{eqnarray}
S_{t+1}&=&S_{t}-\alpha S_{t}\\
I_{t+1}&=&I_{t}+\alpha S_{t}-\beta I_{t}\\
R_{t+1}&=&R_{t}+\beta I_{t}
\end{eqnarray}$$
これでSIRモデルの基本は完成ですが、これだけでは実際の感染症の拡大状況を模擬することができません。より、現実の感染症の拡大を模擬できるように、「感染率は感染者の割合が大きいほど高くなる」と考えて、感染率を次のように変更します。
$$\alpha \longrightarrow \alpha\frac{I_{t}}{S_{t}+I_{t}+R_{t}}=\frac{\alpha}{N}I_{t}$$
ここで、\(S_{t}+I_{t}+R_{t}=N\)は、対象となる全人口を指しているので、時間によらない定数になります。
つまりSIRモデルは、次のような数式で表されます。
$$\begin{eqnarray}
S_{t+1}&=&S_{t}-\frac{\alpha}{N} S_{t}I_{t}\\
I_{t+1}&=&I_{t}+\frac{\alpha}{N}S_{t}I_{t}-\beta I_{t}\\
R_{t+1}&=&R_{t}+\beta I_{t}
\end{eqnarray}$$
なお、感染からの回復率\(\beta\)については、一般的に感染者の数が回復率に影響することは考えられにくいので、今の式のままにしておきます。
それでは、SIRモデルのシミュレーションをしてみましょう。
シミュレーション
ダウンロードしたファイルの「③SIRモデル1」のシートを選択して、人口の増加モデルのように、次のように入力していきます。最初の設定では次のような割合を仮定します。
未感染者 \(S_{1}=1.2億人\)、感染者 \(I_{1}=10万人\)、回復者 \(S_{t}=466人\)、
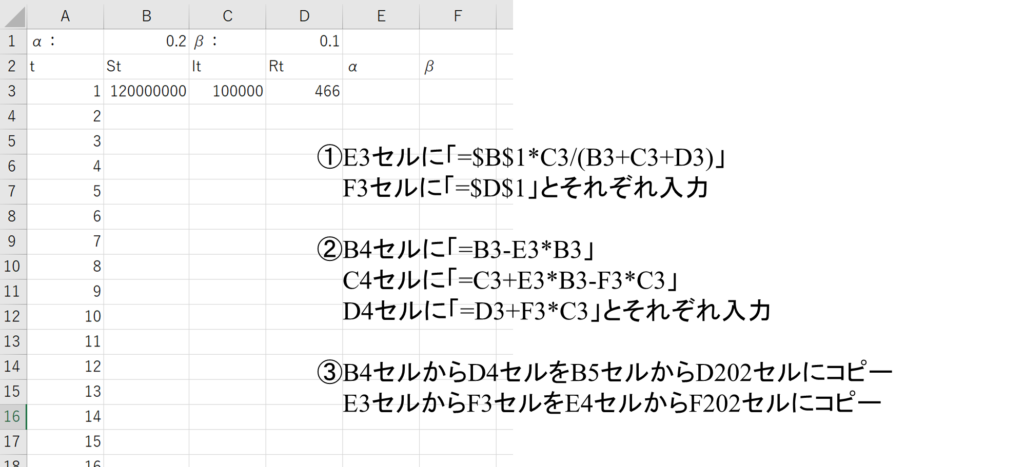
①変化する感染率を計算する。
・E3セルに「=$B$1*C3/(B3+C3+D3)」と入力する。
・F3セルに「=$D$1」と入力する。
※感染率が感染者数の割合で日日で変化することを踏まえて、式に入れずに感染率を計算する列を作りました。
※回復率は変化しませんが、今後修正する場合も考えて、同様に列を作成しました。
②数式モデルを入力する。
・B4セルに「=B3-E3*B3」と入力する。
・C4セルに「=C3+E3*B3-F3*C3」と入力する。
・D4セルに「=D3+F3*C3」と入力する。
③シミュレーションを行う。
B4セルからD4セルをB5セルからD202セルにコピーする。
E3セルからF3セルをE4セルからF202セルにコピーする。
④グラフに表す
・A4セルからD202セルを選択する。
・挿入→グラフ→散布図を選択する。
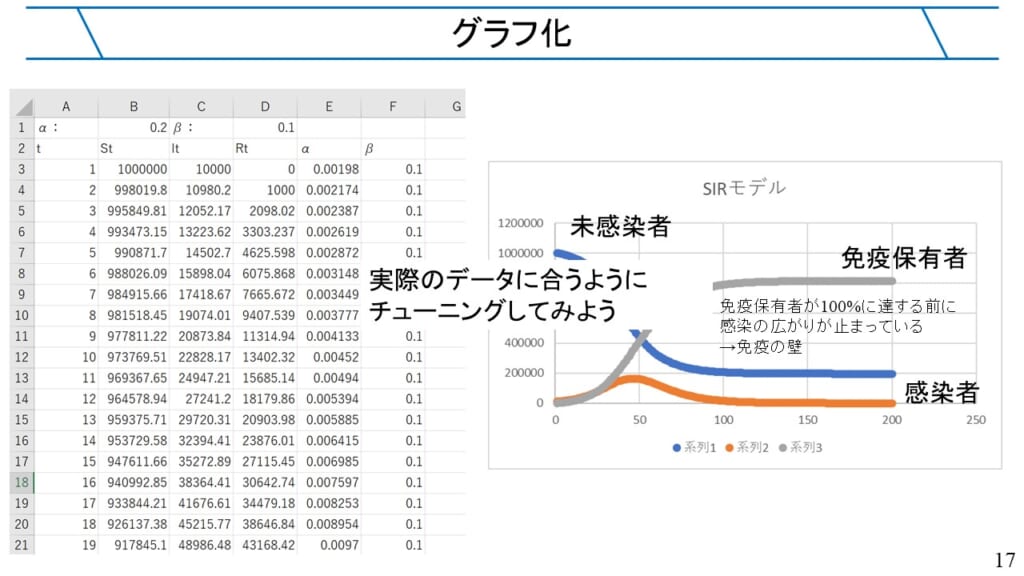
このようなグラフができたでしょうか?
このグラフでは、回復者が一定の割合まで増加すると、全員が感染しなくても、感染者の増加がなくなり感染の拡大が止まっていく様子が分かると思います。これがいわゆる「免疫の壁」と呼ばれるものになります。SIRモデルでは単純なモデルですが、免疫の壁を模擬できることから、感染症の拡大モデルとして大事な役割を果たしています。なお、SIRモデルを作成した際には、感染率が感染者の割合に応じて変化するようにモデルを修正しましたが、修正を行わない場合は、このような特徴が現れず、全員が感染するまで感染は拡大し続けます。

パラメータの調整
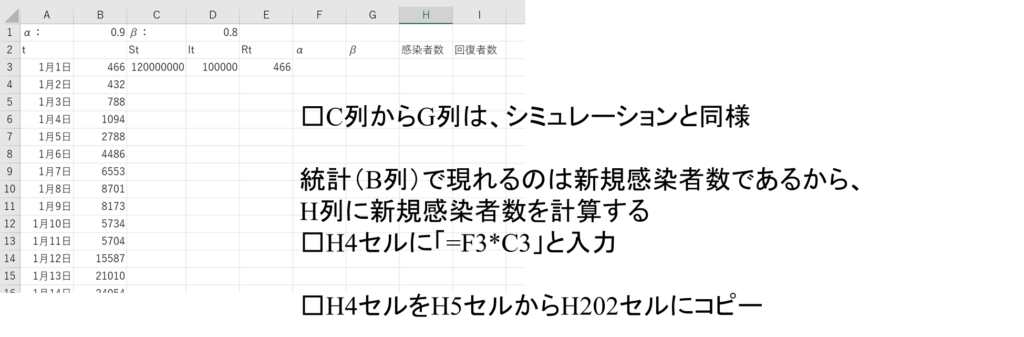
次は実データと比較して、パラメータの調整を行ってみたいと思います。ダウンロードしたファイルの「④SIRモデル2」シートを選択してください。このシートのB列には、新型コロナ感染症が拡大した際のデータが入力されています。このデータに一致させることができるか見ていきましょう。
C列からG列までのシミュレーションは1列ずれていること以外、先ほどの例と同じのため、同じように入力してください。新型コロナウイルス感染症の実データは新規感染者数となっているため、比較のためには改めて計算が必要になります。次のように計算してください。
①新規感染者数の計算
・H4セルに「=F3*C3」と入力する。
②H4セルに