第1節 モデリング&シミュレーションとは
この講座では、M&S(モデリング&シミュレーション)の手法を通して、数学や物理の世界を広げることを目標に解説を行います。
高校で習う数学や物理はとても限定的です。例えば数学で習う積分は、教科書に出てくる簡単な関数でも積分を求めることは大変に難しかったり、実はほとんどの関数の不定積分を簡単な関数で表すことが困難だったりします。同様に物理でも、時間軸での運動の評価は、運動方程式を習っているにも関わらず、等加速度運動や単振動等の限定的な運動のみでしかできません。
特に最先端の科学の結果等から複雑なシミュレーション結果を目にする機会も多くあり、高校で習う数学や物理とのギャップや無力さを感じます。でも、ほんとはそんなに大きなギャップはなく、ちょっとした工夫をすればそのギャップを埋めることができるのです。
そのために必要なものは、数列の考え方とコンピューターです。特に数列については教科書で習うような、一般項や和の公式は必要ありません。数列という概念を理解できれば、応用は可能です。またコンピューターは一人一台タブレットの時代が到来したため、自由に活用できる状況だと思います。そこでこの講座では、プログラムを用いずモデリングやシミュレーションを行うために、エクセルを利用したいと思います。
モデリングとは
モデリングとは、自然現象や社会現象等における事象を表現する抽象化したモデルを作成することを指します。モデルには次のような、さまざまな種類が存在します。
(1)数学モデル 自然現象や社会現象を表した数式、データベース等、物理的な実態を伴わないモデル
(2)物理モデル システムの一部や全部を物理的に模擬した装置であるが、数学モデルと併用して用いることも多い
(3)図形モデル 現象の状態を図形や記号を用いて表現したもの

シミュレーションとは
シミュレーションとは、作成したモデルを使い、現象を再現して必要なデータを得ることを言います。シミュレーションと言えば、コンピューターシミュレーションを指すように思いますが、いろいろな形があります。以下はほんの一例ですが、さまざまなシミュレーションが行われています。
(1)フライトシミュレーション 運動方程式や空力データベースを元に飛行状態を模擬します。一部の装置を物理的に模擬する場合もあります。
(2)全機静強度試験 実際に機体の構造を模擬した実大模型に力を加えて、各部位にかかる力を測定します。
(3)机上シミュレーション 災害等の対応の訓練や手順の確認のために、図表やシナリオを用意して行います。

第2節 エクセルの使い方(基本的な計算)
エクセルとは、マイクロソフト社がWindows、macOS、iOSおよびAndroid向けに開発・販売している表計算ソフトです。Microsoft Wordとともに、同社の「Microsoft Office」の中核をなすアプリケーションであり、多くの会社で用いられています。
日本では、ワープロ代わりに使われることも多ですが、極めて高い計算能力があるのでそれだけで終わってしまうのはもったいないと思います。まずは最初に、エクセルの使い方について簡単に説明します。エクセルが使える人は、第3節のグラフの描き方に進んでください。
エクセルは巨大な表からなります。表のことをスプレッドシートや単にシートと言います。シートの横の並びを行、縦の並びを列といいます。また表を構成する1つ1つの枠を、セルと呼びます。セルには1つ1つ名前がついています。下の例では、第11行の第N列のセルを指しているため、N11セルと呼びます。
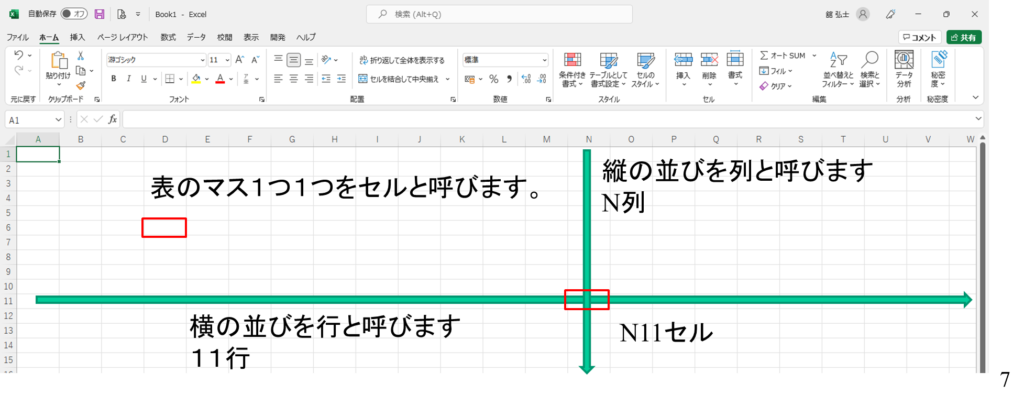
それでは次のファイルをダウンロードして、エクセルを使ってみましょう。
①エクセルで計算する。
基本的な演算方法
エクセルでは次のような演算子を使って計算します。
× → *
÷ → /
√ → sqrt( )
ab → a^b
問題①ー1:基本計算
〇A4セルに半径2の球の体積を計算してみよう。
・A4セルに「=4/3Pi()2^3」と入力する

〇B6セルからB14セルに√1から√9の値を計算してみよう。(セルの相対参照)
②セルを参照する
・B6セルに「=sqrt(A6)」と入力する
・B6セルを右クリックしてコピーを選択する
・B7セル左クリックしたままB14セルまで選択する
・選択した範囲の上で右クリックして、貼り付けを選択

〇B16セルの値に1から9を掛けた値をB17セルからB25セルに計算してみよう。
※相対参照と絶対参照
・B17セルに「=$B$16*A17」と入力する
・B17セルを右クリックしてコピーを選択する
・B18セル左クリックしたままB25セルまで選択する
・選択した範囲の上で右クリックして、貼り付けを選択

第3節 エクセルの使い方(グラフの描き方)
グラフを描くといえば、高校1年生では2次関数を平方完成し、2年生では三角関数や指数対数関数のグラフの一般的な形状を勉強し、最後に2年生から3年生にかけて微分法をならい、増減表を作ることで正確なグラフを描くことができるようになりました。
グラフを描くために必要な道具はすべて揃ってどんなグラフも描ける気がしますが、実は\(f'(x)=0\)が解けなければグラフは描けないので、実はかなり制限された道具なのです。しかし、コンピュータを使えばもっと簡単にグラフを描くことができます。特殊なアプリケーションは必要ありません。MS エクセルがあれば十分です。
\(y=x^2\)のグラフを最初に描いた方法を思い出してみましょう。次の図のように、\(x\)の値を、\(x=-3\)、\(x=2\)、\(\cdots\)、\(x=3\)のように変化させたときの\(y\)の値を計算して表にし、その値をxy平面上に表示して滑らかにつないだのではないでしょうか。
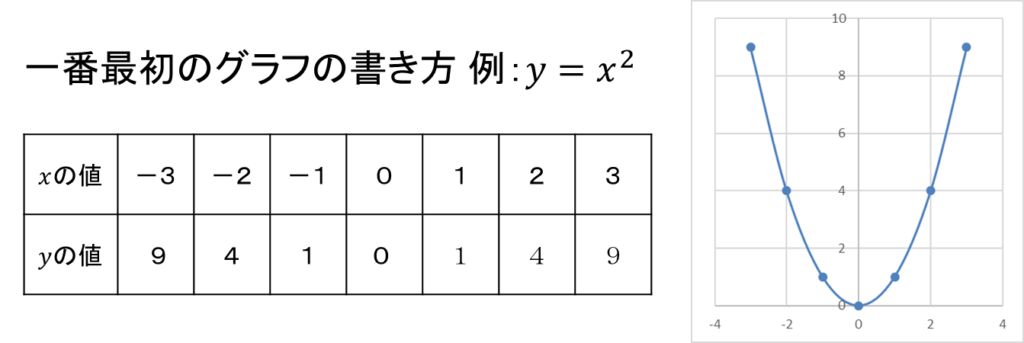
この方法と同じ方法でグラフを描けばいいのです。しかもコンピューターを使うことができるので、もっと細かく計算することができます。
引き続き先ほどダウンロードしたファイルを使って、今度はグラフを描いてみましょう。
まずは、\(y=x^2\)のグラフを\(0≦x≦1\)の範囲で描いてみます。先ほどの例では1おきに値を計算しましたが、大雑把なので、0.01おきに計算します。このことを\(\Delta x=0.01\)と表します。
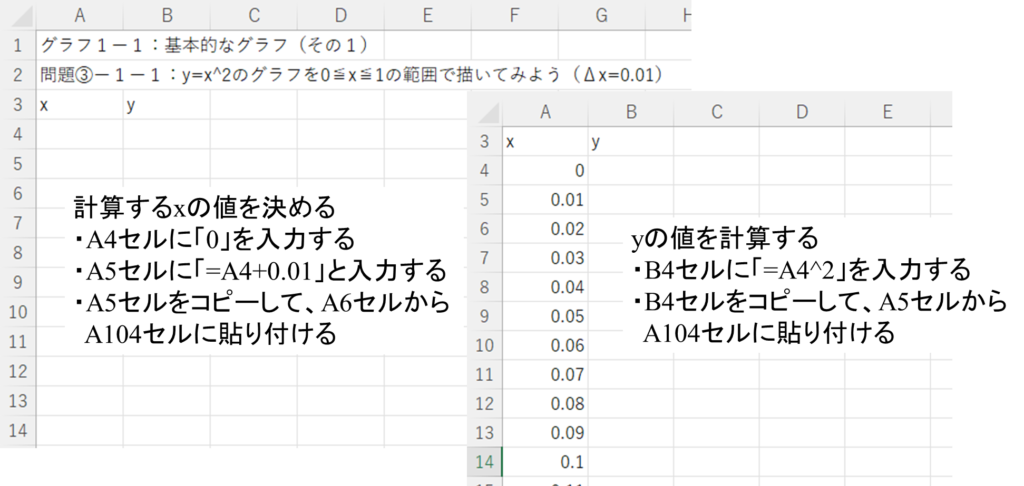
①計算する\(x\)の値を準備する。
・A4セルに「0」と入力する。
・A5セルに「=A4+0.01」と入力する。
・A5セルをコピーして、A6セルからA104セルに貼り付ける。
②\(y\)の値を計算する。
・B4セルに「A4^2」と入力する。
・B5セルをコピーして、B6セルからB104セルに貼り付ける。
以上の操作で、グラフを描く元となる表が完成しました。
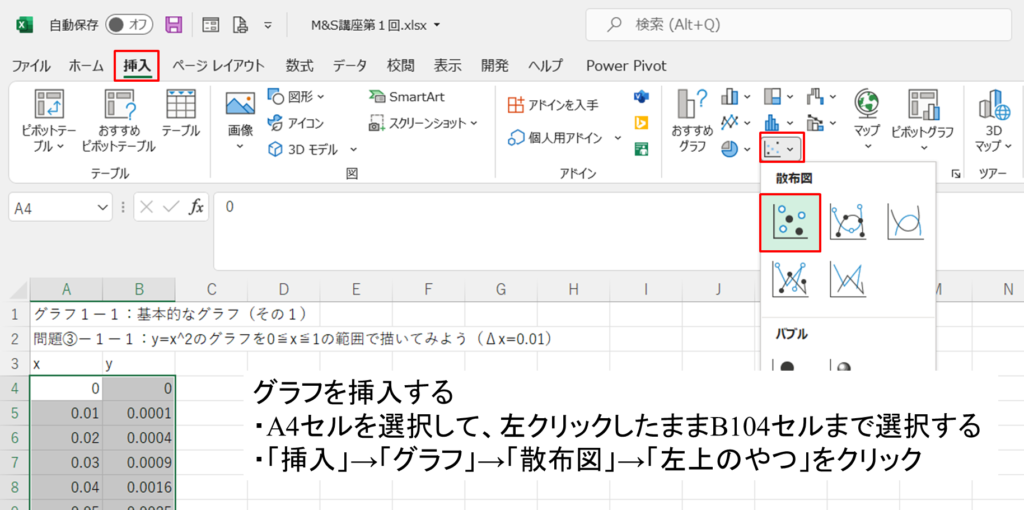
③グラフを作成する。
・A4セルからB104セルまでの範囲を選択する。
・「挿入」→「グラフ」→「散布図」→「左上のグラフ」をクリックする。
※本講座では点の散布図を選びましたが、好きなものを選んでください。左上のグラフは計算した点しか表示しませんが、他のグラフは計算していない点も、直線または曲線で補完して表示します。
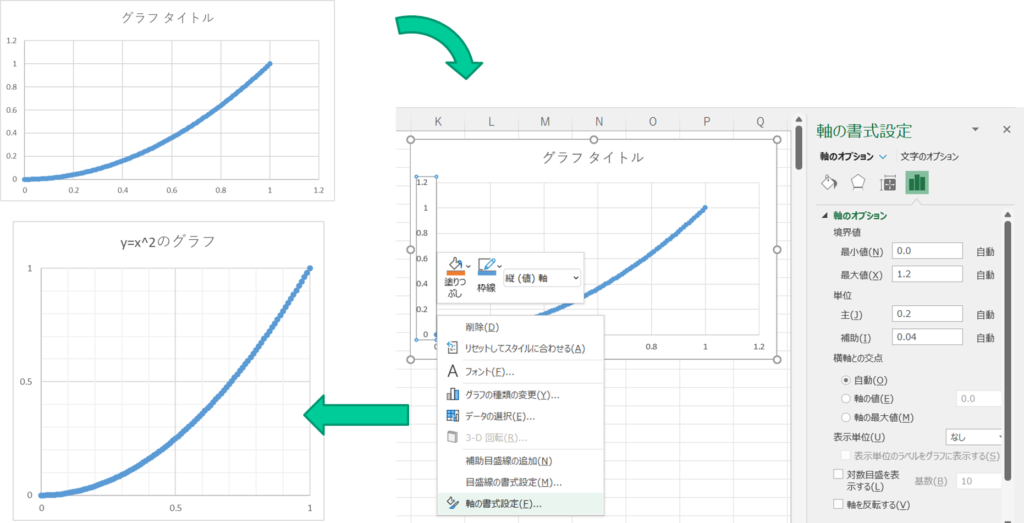
④グラフを修正する。
※より分かりやすいグラフにするために、x軸を修正してみます。
・グラフのx軸を右クリックして、軸の書式設定をクリックする。
・x軸の書式設定ウィンドウで、設定を変更する。
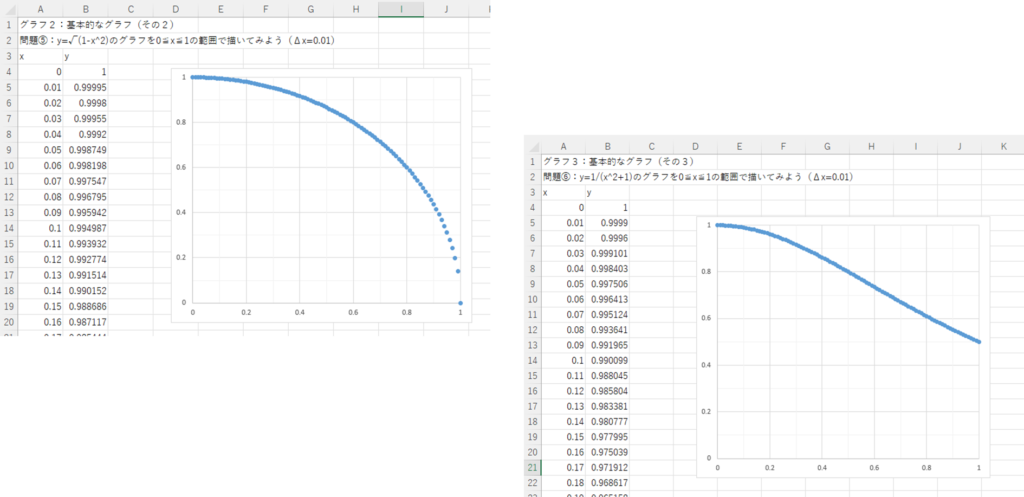
⑤いろいろなグラフを描く
シートを変えると他にもいろいろな関数が用意されているので、それらのグラフを描いてみてください。
⑥複数のグラフの同時表示
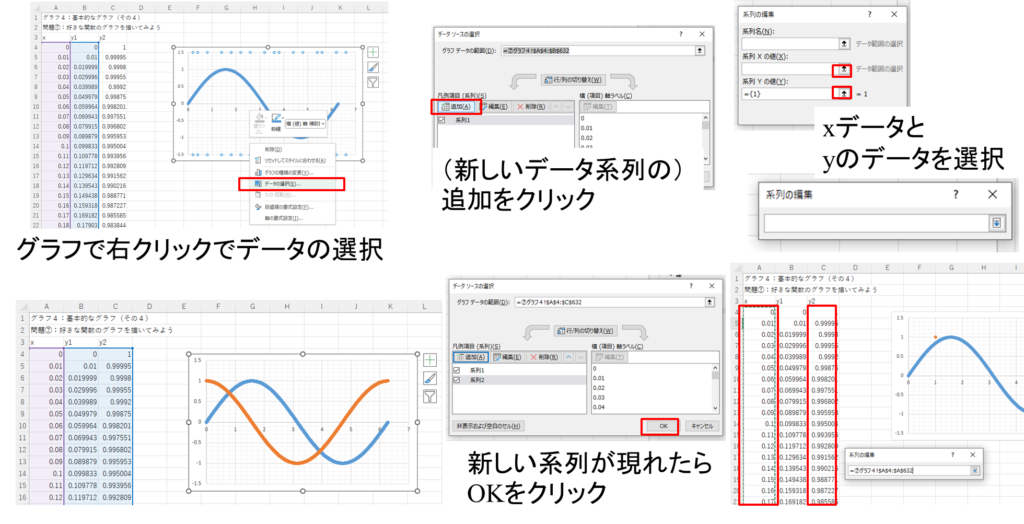
同じ座標平面に2つ以上のグラフを同時に表示させる場合は次のように追加します。
・2つのグラフのxデータとyデータを準備する。
・グラフを右クリックして、「データの選択」をクリックする。
・現れたウィンドウで、(新しいデータ系列の)「追加」をクリックする。
・xデータとyデータを選択するウィンドウが現れるので、それぞれを選択する。
・新しい系列が現れたら、OKをクリックする。
以上のようにすれば、増減表を描かなくても、簡単にきれいなグラフを描くことができます。
第4節 エクセルを使った積分
いよいよ積分まで到達しました。大雑把に言えば、積分と言えば曲線とx軸で囲まれた部分の面積を求めることを意味します。そのため高校3年生で習う積分には非常に面倒な計算が必要になります。しかし、面積を求めるだけなら、エクセルを使えば簡単にできます。グラフが分かれば、誰でも計算できるのです。
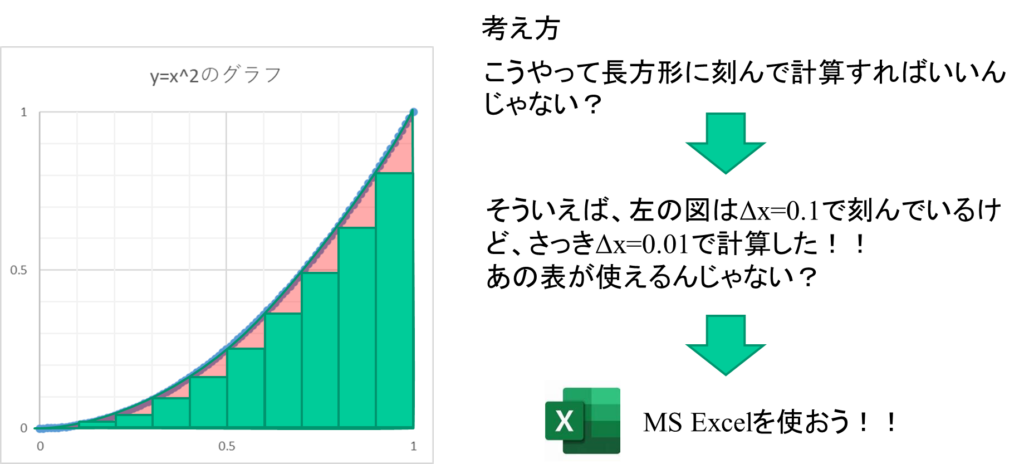
考え方は、曲線とx軸で囲まれた図形を下図のように縦に刻んで、その刻んだ部分を長方形とみなして、その面積を足し合わせればいいわけです。しかし、その準備はすでにできているのです。なぜなら、縦に刻んだ長方形1つ1つの高さは、先ほど計算した表のyの値になります。また長方形の横幅は\(\Delta x=0.01\)となるからです。
このため、この細長い長方形の面積は高さと横幅を掛け算すれば求められるので、それらを足し合わせれば、面積を求めることができます。これはエクセルが得意な計算です。では実際にやってみましょう。
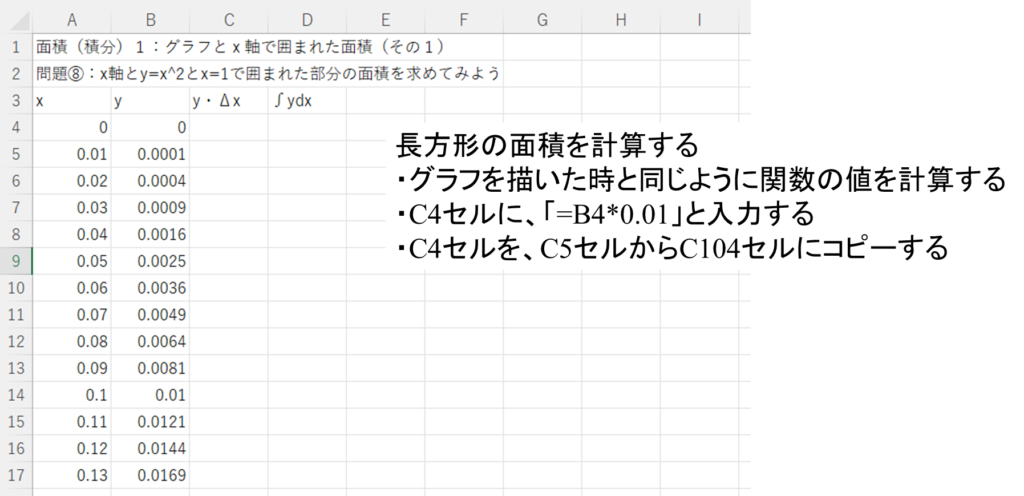
①長方形の面積を計算する。
・グラフを描いた時と同じように、関数の値を計算する。
・C4セルに「=B4*0.01」と入力する。
・C4セルを、C5セルからC104セルにコピーする。
②足し合わせて面積を求める。
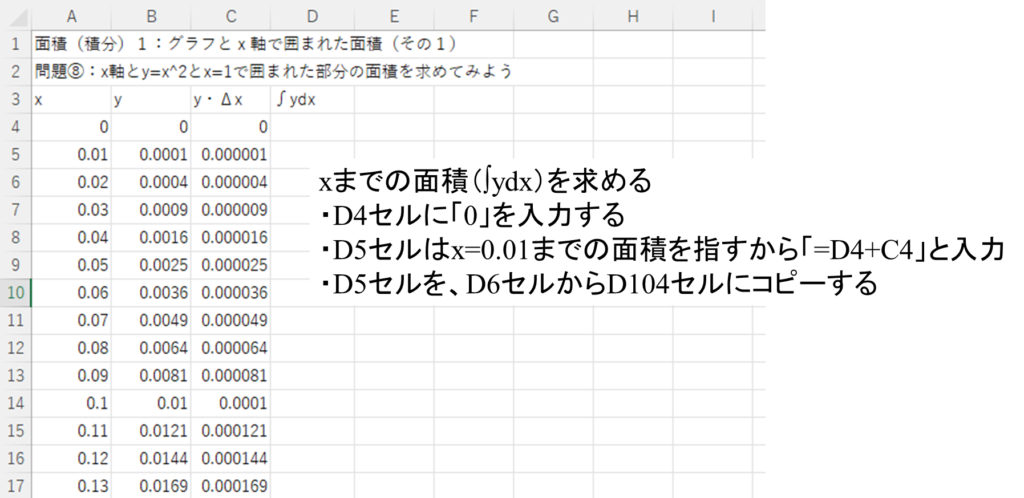
※C列をいきなり全部足し合わせて面積を求めてもいいのですが、順番に足すことで\(\int_{0}^{x}f(t)dt\)が求まるので、そちらを計算してみましょう。
・D4セルに「0」を入力する。
・D5セルに「=D4+C4」と入力する。
・D5セルを、D6セルからD104セルにコピーする。
※このように入力することで、C列にはそれまでのB列の値の和が計算されるのです。
③積分の完成
D104セルの値が、放物線とx軸に囲まれた部分の面積になります。
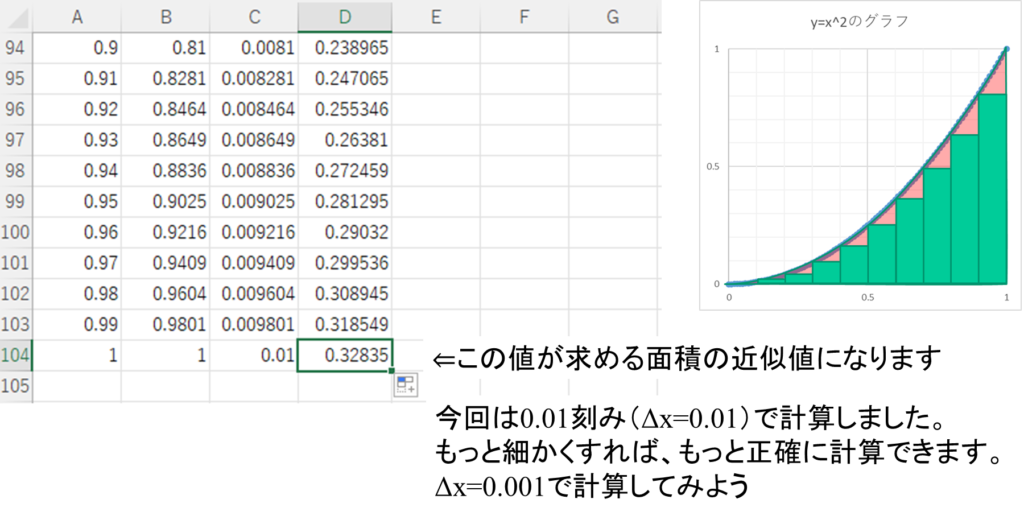
④より細かく刻む
先ほどの例では\(\Delta x=0.01\)で計算しましたが、細かく刻めば刻むほどより正確な面積が出そうです。次は、\(\Delta x=0.001\)で計算してみましょう。
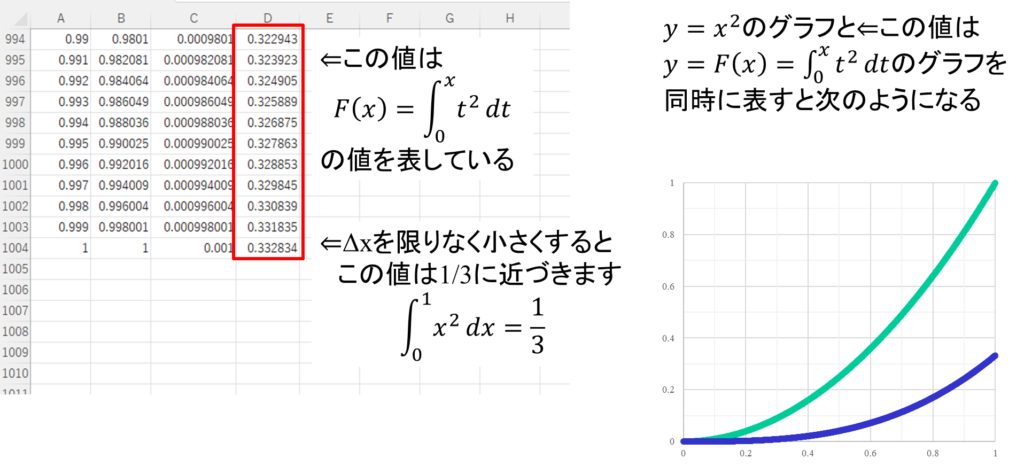
すると、面積は0.332834となります。積分を勉強した人は分かると思いますが、正確な値は\(\frac{1}{3}\)です。かなり近い値が求められたと思います。
またD列の値を関数としてグラフに表すと、右下の青線のようなグラフが得られます。これも積分を勉強した人は分かると思いますが、理論的には\(y=\frac{1}{3}x^3\)のグラフになるはずです。
以上のように関数の値さえわかっていれば、エクセルを使うことで、長方形の面積を求めるための掛け算と、長方形の面積を足し合わせる足し算だけで、グラフを積分することができます。
これは凄いことではないでしょうか?例えば\(\int_{0}^{1}\frac{dx}{x^3+1}\)を求めるだけで、とても骨が折れる計算をしなければなりませんでした。また、積分をいくら勉強しても、\(\int_{0}^{\pi} \sin x^2 dx\)を簡単な関数で求めることは出来ません。また、関数ですら表されない数値データの列に至っては手の出しようがありません。しかし、エクセルを使えば、簡単に積分ができるのです。
もちろん、実際の関数を正確に積分することは非常に大事なことですが、エクセルを使えば、簡単に積分できてしまうことも同じように大事なことではないでしょうか。
最後は演習ファイルのシートにある、いろいろな関数について積分してみてくてださい。
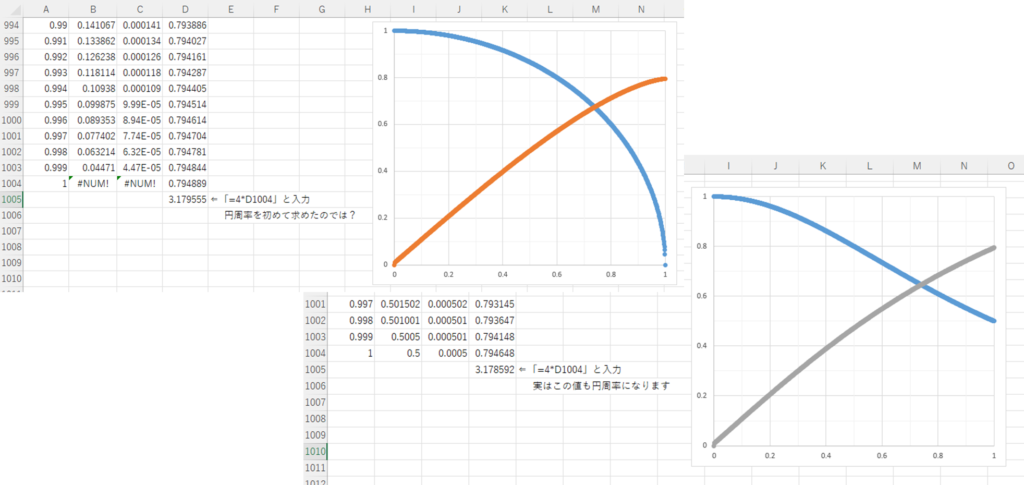
最後にこちらが模範解答です。
第5節 パラメトリックなグラフの描画(おまけ)
最後にパラメトリックなグラフを描く練習をしてみましょう。
例えば次のような式を考えます。
$$\left\{\begin{array}{ccl}x&=&t^3-t\\y&=&t^2\end{array}\right.$$
この式は、\(t\)を変化させると\(x\)と\(y\)が変化することから、xy平面上を動く点を表していると考えます。簡単に、\(t=-2\)、\(t=-1\)、\(\cdots\)、\(t=2\)と変化させたときの\(x\)と\(y\)の値は次のようになります。この刻み幅をもっと細かくして、グラフを描くと右のようなグラフになることが分かります。
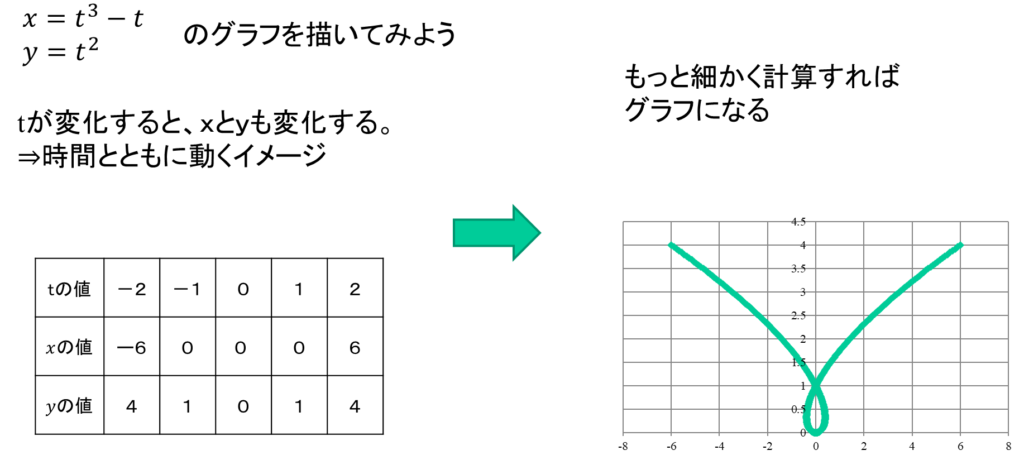
実際に次のファイルをダウンロードして、パラメトリックなグラフを描いてみましょう。
頑張れば、100均で売っている定規の曲線もパラメータ表示で表すことができます。
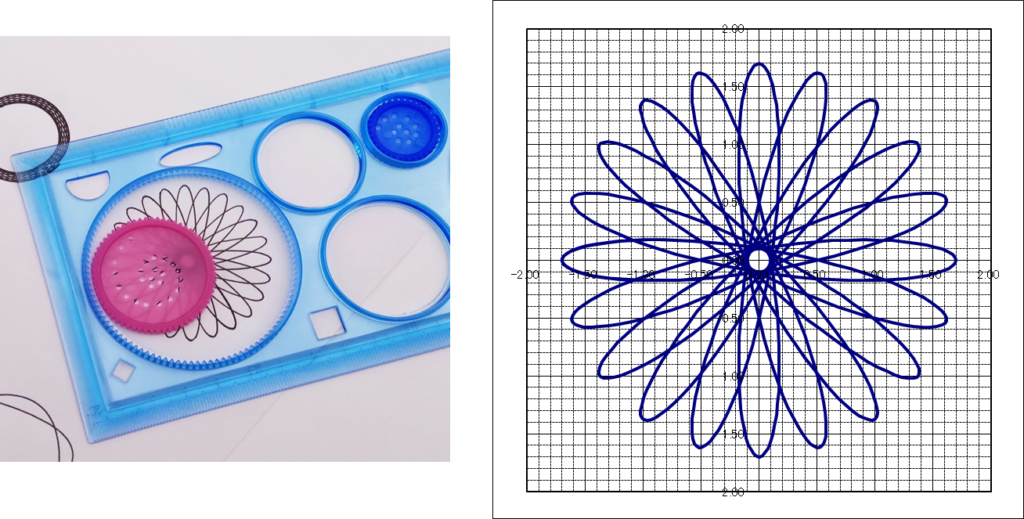
興味がある人は頑張って計算してみてください。
